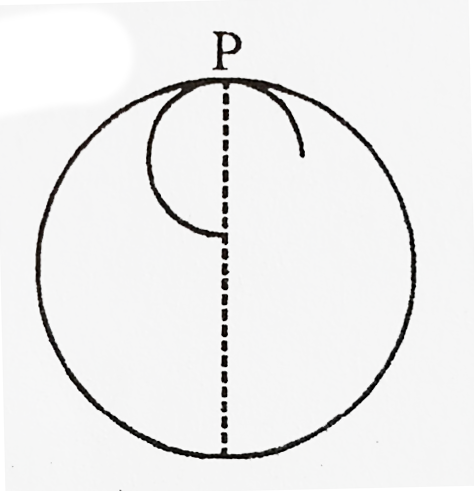
A spherical planet (density = $ρ$ ) of radius R has a spherical cavity of radius R/3, as shown
(a) A small body is released at point P. How much time would it take to reach the lower surface of the cavity ?
(b) A small body of mass m is placed at a distance 2R above point P, on the dotted line extended upwards. What force does the planet exert on the body ?

Text Solution

Verified by Experts

The correct Answer is:(a) $\sqrt{\frac{3}{2 ρ}} π G$ , (b) $\frac{184}{1323} M G ρ π R$

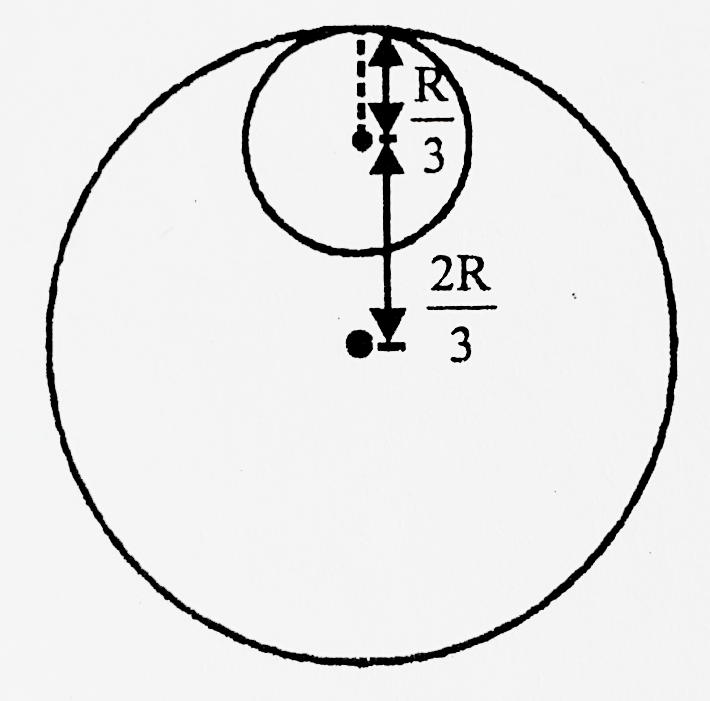
(a) Net E constant inside covity
$E = \frac{8}{9} π ρ G R$
So $\frac{2 R}{3} = \frac{1}{2} a t^{2}$
$T = \sqrt{\frac{2 \times 2 \times R / 3}{\frac{4}{3} π G P \frac{2 R}{3}}} = \sqrt{\frac{3}{2 π ρ G}}$
(b) $m ⎡ ⎢ ⎢ ⎢ ⎣ \frac{G . \frac{4}{3} π R^{3} P}{{(3 R)}^{2}} - \frac{G . \frac{4}{3} π {(\frac{R}{3})}^{3} P}{{(\frac{7 R}{3})}^{2}} ⎤ ⎥ ⎥ ⎥ ⎦ = \frac{184}{1323} M G P π R$

Updated on:21/07/2023

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
A $+ Q, - Q$
B $- Q, + Q$
C $Q, - Q$
D $+ Q, 0$

BANSAL-GRAVITATION-EXERCISE -3 [Miscellaneous Exercise]

Home
Ask Doubt
Profile