Four masses (each of $m$ ) are placed at the vertices of a regular pyramid (triangular base) of side 'a'. Find the work done by the system while taking them apart so that they form the pyramid of side '2a'.

Video Solution

Text Solution

Verified by Experts

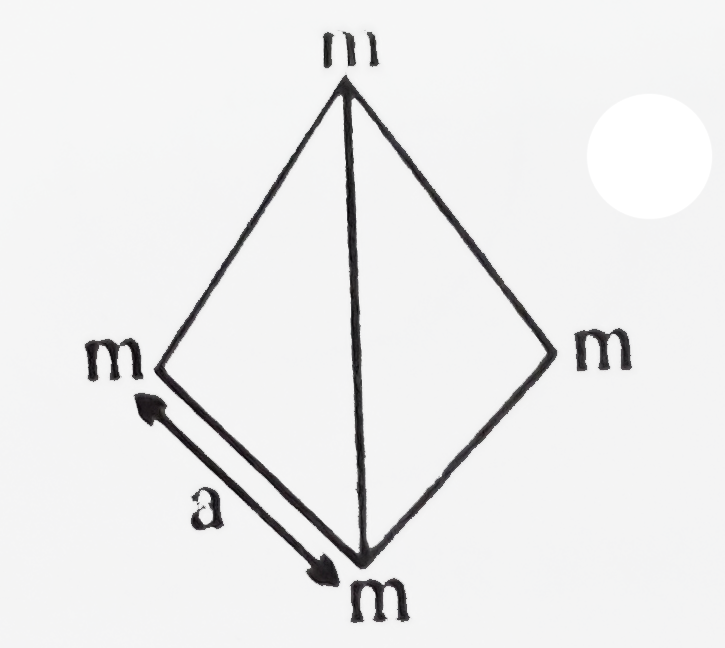
The correct Answer is: $- \frac{3 G m^{2}}{a}$

External work done $= Δ U$
$= U_{f} - U_{i} = - \frac{6 G m^{2}}{2 a} - (- \frac{6 G m^{2}}{a}) = + \frac{3 G m^{2}}{a}$
work done by system $= - \frac{3 G m^{2}}{a}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three particles, each having a charge of $10 μ C$ , are. placed at the vertices of an equilateral triangle of side. 10 cm. Find the work done by a person in pulling them apart to infinite separations.
A $27 J$
B $2.7 J$
C $- 2.7 J$
D $- 27 J$
Question 2 - Select One or More
Four point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is $r$ .
AGravitation field at centre at zero
BGravitation potential at centre is $\frac{- 4 G m}{r}$
CGravitation potential energy of system in $\frac{- 6 G m^{2}}{r}$
DGravitation force on one of the point mass is $\frac{\sqrt{6} G m^{2}}{r^{2}}$
Question 3 - Select One
Four particles each of mass m are placed at the vertices of a square of side $l$ . the potential at the centre of square is
A $- 2 \sqrt{2} \frac{G m}{l}$
B $- 3 \sqrt{2} \frac{G m}{l}$
C $- 2 \frac{G m}{l}$
D $- 4 \sqrt{2} \frac{G m}{l}$

BANSAL-GRAVITATION-EXERCISE -3 [Miscellaneous Exercise]

Home
Ask Doubt
Profile