Length v/s Temperature graph of A & B is given below. Find the relation between αA&αB.

αA>αB
αA=αB
αA<αB
can't say
The correct Answer is:C
ΔL=LαΔT
slope ⇒ΔLΔT=Lα
(Slope)A<( Slope)B,L(A)αA=LBαB
∵LA=LB therefore ∴(αA<αB)
Topper's Solved these Questions
Similar Questions
Two composite rods made by A & B and C & B materials as shown. When we increase the temperature ΔT, relation between final lengths of rod becomes L1<L2. Find the relation between αA and αC.
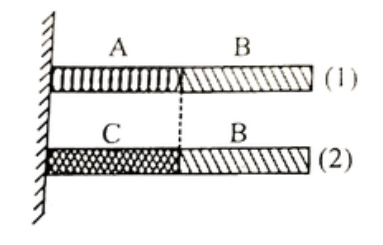
View Solution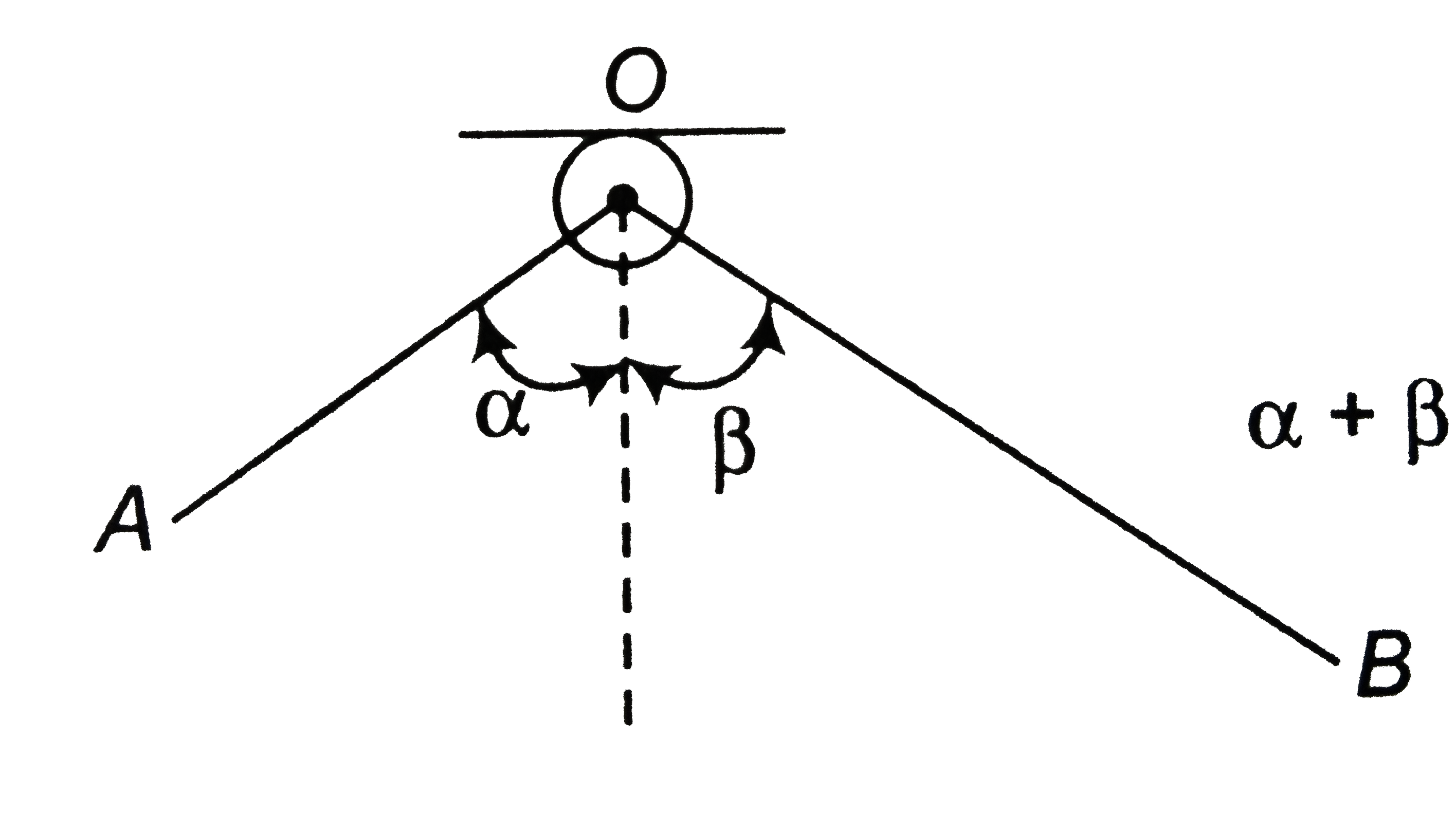
A uniform L shaped rod of mass 3 m is hinged at point O. length OB is two times the length OA. It is in equilibrium.
Find
(a). Relation between α and β
(b). Net hinge force.
View Solution
A uniform L shaped rod of mass 3 m is hinged at point O. length OB is two times the length OA. It is in equilibriu.
Find
(a). Relation between α and β
(b). Net hinge force.
View SolutionA cubical block of co-efficient of linear expansion αs is submerged partially inside a liquid of co-efficient of volume expansion γl. On increasing the temperature of the system by ΔT, the height of the cube inside the liquid remains unchanged. Find the relation between αsandγl.
View SolutionA cubical block of co-efficient of linear expansion αs is submerged partially inside a liquid of co-efficient of volume expansion γl. On increasing the temperature of the system by ΔT, the height of the cube inside the liquid remains unchanged. Find the relation between αsandγl.
View SolutionFind the relation between current gain α and β of transistor.
View SolutionDiagram below depicts an experiment to find the effect of temperature on the rate of photosynthesis. The average number of bubbles per minute at each temperature is given in the table.

Plot a graph to show the relation between the rate of photosynthesis and temperature.
View SolutionIf ∣∣∣xyαβ∣∣∣=0, then, find the relation between x and y.
View SolutionTwo rods of different metals of coefficient of linear expansion α1 and α2 and initial length l1 and l2 respectively are heated to the same temperature. Find relation in α1,α2,l1 and l2such that difference between their lengths remain constant.
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
View Solution
