Gravitational force on mass m placed at origin is:-

GM2a2ˆi
GM2a2ˆj
GM2a2(ˆi+√3ˆj2)
√3GM2a2(√3ˆi+ˆj2)
The correct Answer is:D

FR=(√3)(GM2a2)(√3ˆi+ˆj2)
Topper's Solved these Questions
Similar Questions
Mass particles of 1 kg each are placed along x-axus at x=1,2,4,8,....∞. Then gravitational force o a mass of 3 kg placed at origin is (G= universal gravitation constant) :-
View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View Solution
Knowledge Check
Mass particles of 1 kg each are placed along x-axus at x=1,2,4,8,....∞. Then gravitational force o a mass of 3 kg placed at origin is (G= universal gravitation constant) :-
A4GB4G3C2GD∞A large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
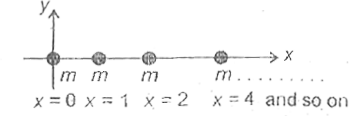 AGm2B43Gm2C23Gm2D54Gm2
AGm2B43Gm2C23Gm2D54Gm2
If two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionA large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
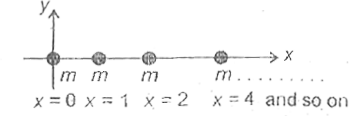
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View SolutionThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View Solution
