A metallic wire carrying a current I is bent into a form as in the figure. The circular portion MNO of the wire is of radius r and the straight portion MO subtends an angle 2θ at the centre C. Find the magnetic field at C due to the whole conductor.

μ02π.Ir(π−θ+tanθ), downward direction
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - ENTRANCE CORNER
7 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - MULTIPLE CORRECT ANSWERS TYPE
7 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - PROBLEM SET-II
20 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
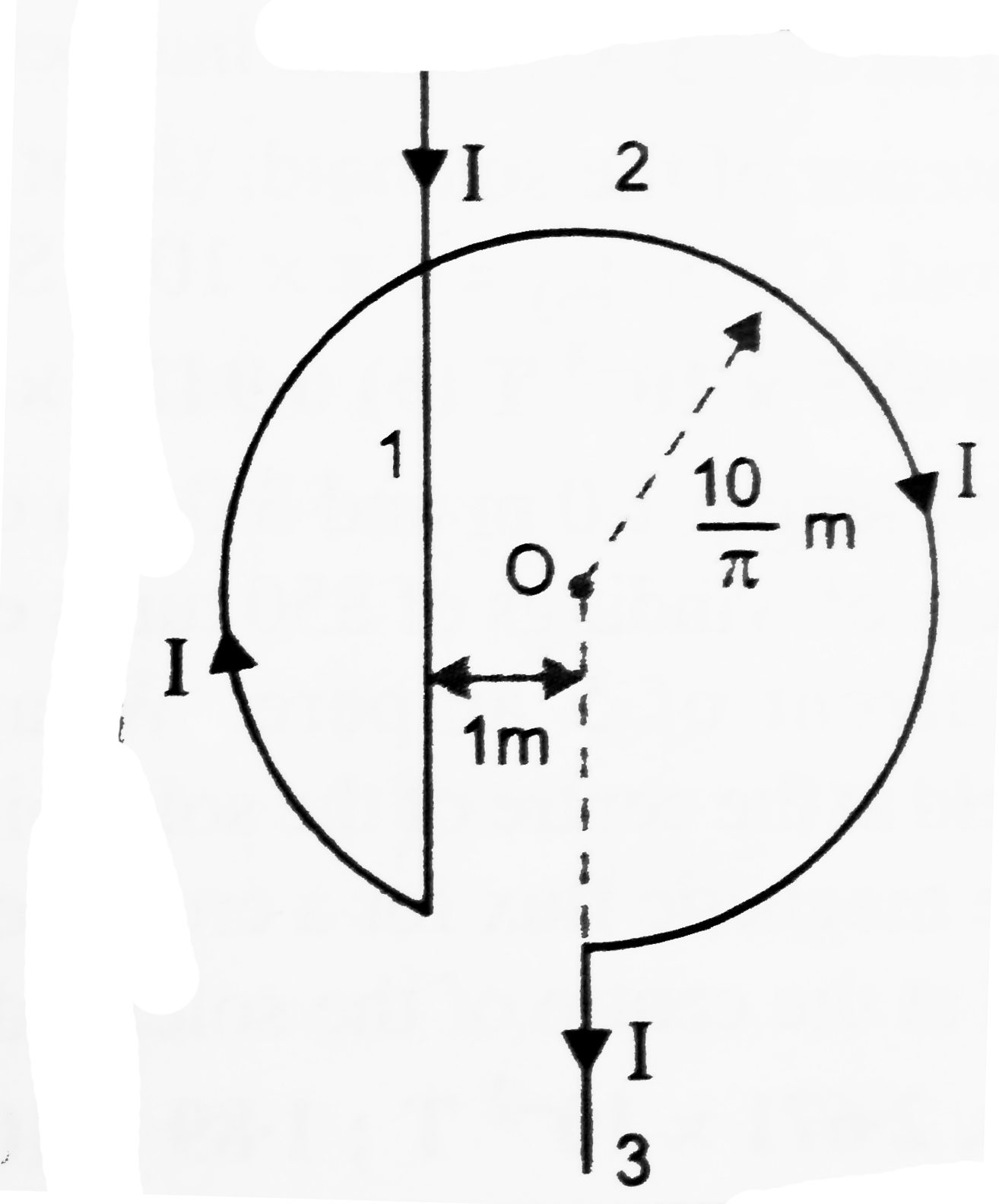
A long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View Solution
Knowledge Check

A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2Current I is flowing in a conductor shaped as shown in the figure. The radius of the curved part is r and the length of straight portion is very large. The value of the magnetic field at the centre will be
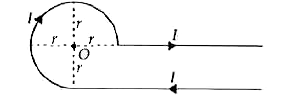 Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
A piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
View SolutionA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
View Solution
