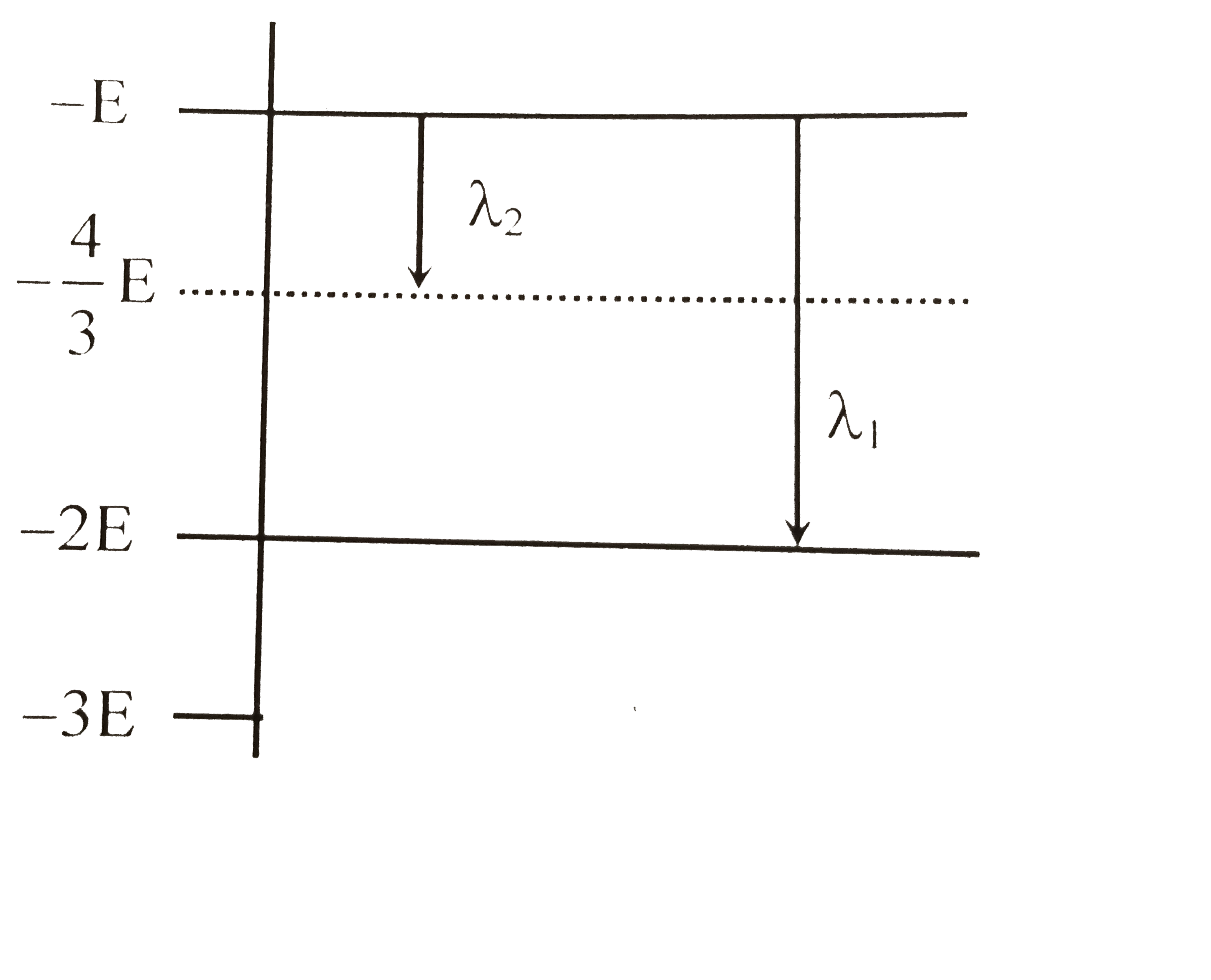
Some energy levels of a molecule are shown in the figure.
The ratio of the wavelengths r=λ1/λ2 is given by

r=43
r=23
r=34
r=13
The correct Answer is:D
According to Bohr's postulate,
ΔE=hv=hcλor,λ=hcΔE
In this case, r=λ1λ2=ΔE2ΔE−1=(−43E)−(−E)(−2E)−(−E)=13
Topper's Solved these Questions
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (AIPMT)
2 Videos
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (NEET)
3 Videos
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (WBJEE)
6 Videos
- ALTERNATING CURRENT BOOK - CHHAYA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CBSE SCANNER
33 Videos
- ATOMIC NUCLEUSBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMIC NUCLEUSEXERCISE - CBSE SCANNER
14 Videos
Similar Questions
Knowledge Check
Some energy levels of a molecule are shown in the fig. The ratio of the wavelengths r=λ1/λ2, is given by
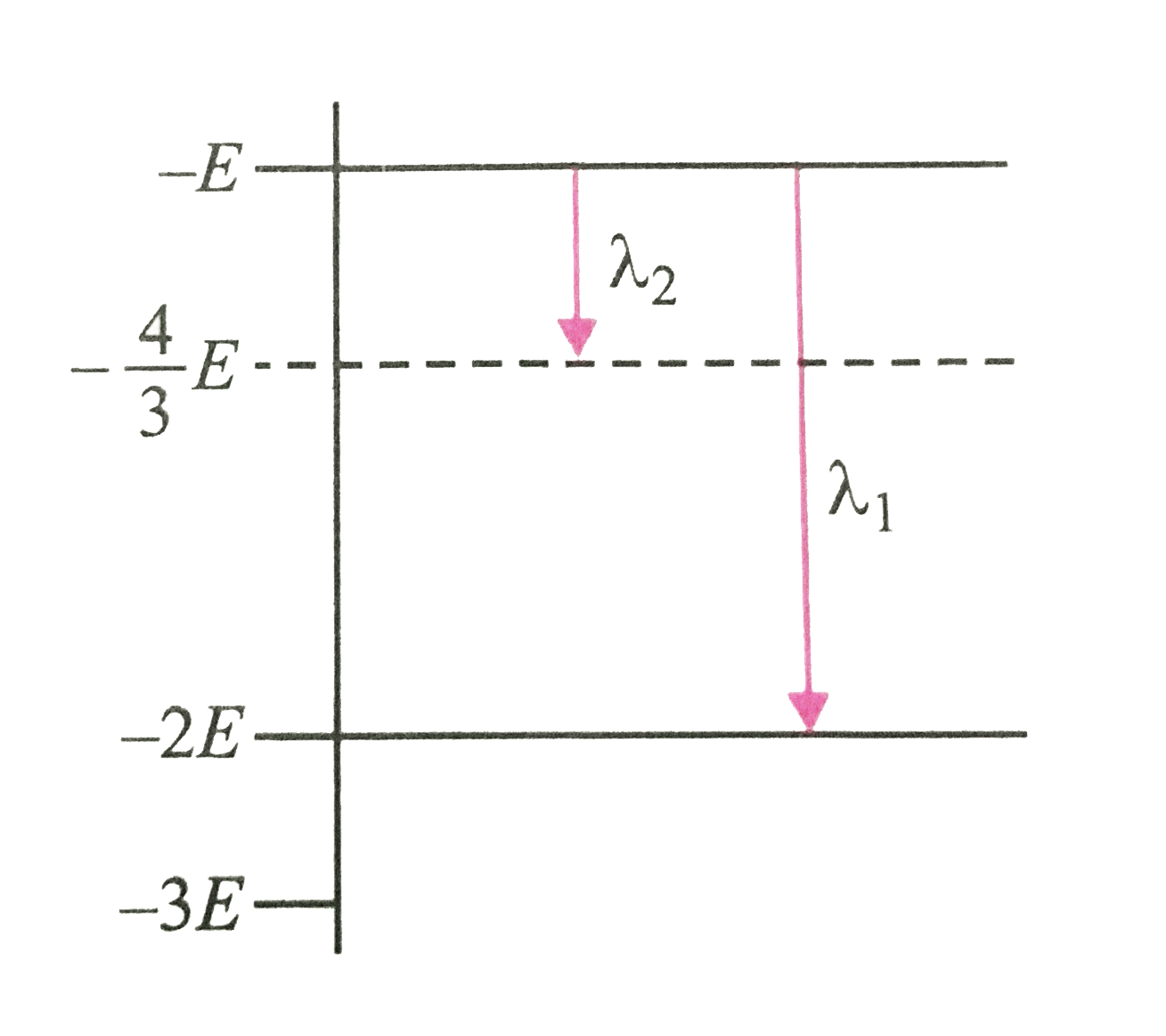 Ar=34Br=13Cr=43Dr=23
Ar=34Br=13Cr=43Dr=23The energy of a photon of wavelength λ is given by
AhλBchλCλhcDhcλThe energy of a photon of wavelength λ is
AhcλBhcλCλhcDλhc
The energy of a photon of wavelength λ is
View SolutionIf λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
View SolutionIf λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
View Solution