A particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is
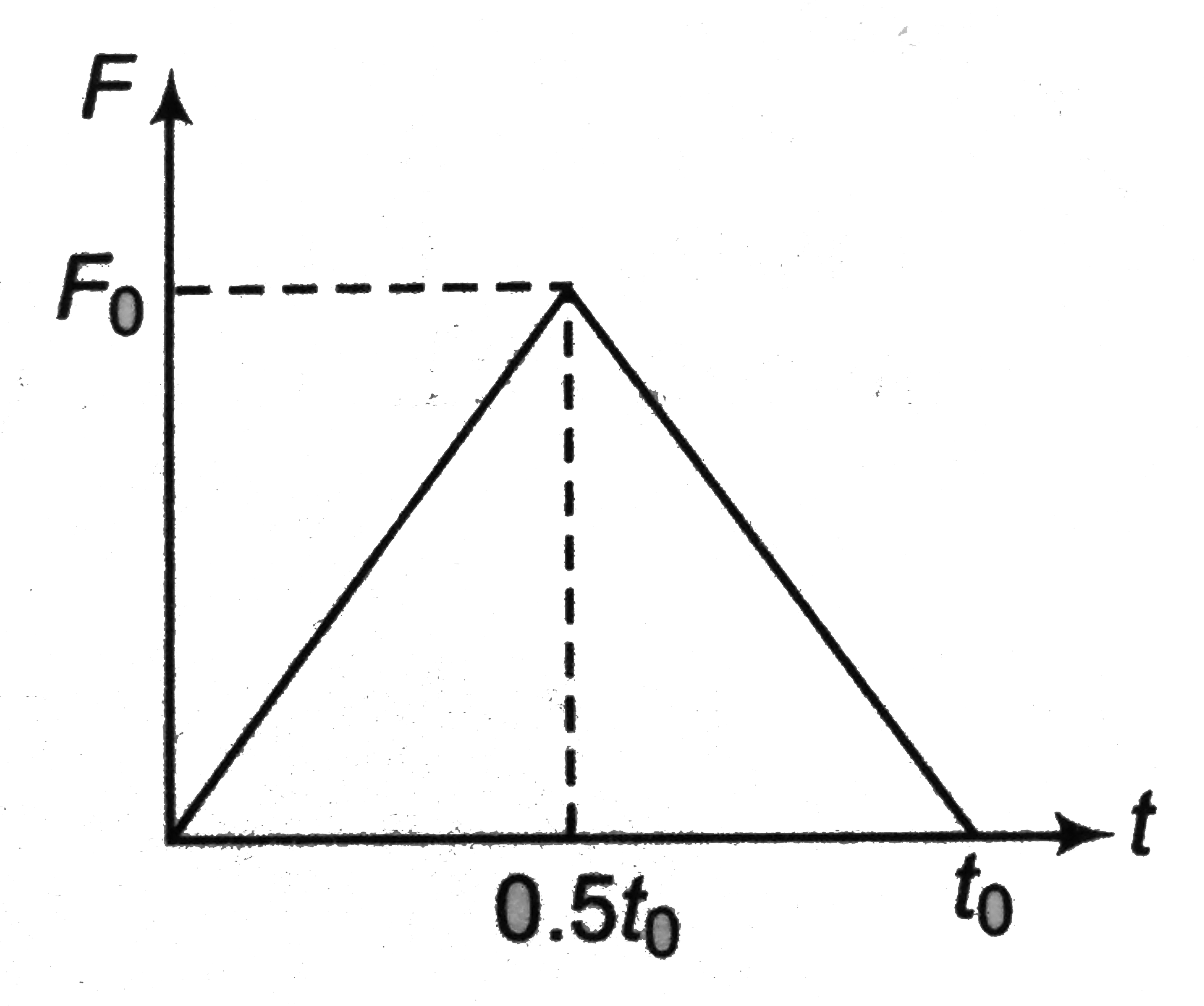
mu/T
2mu/T
mu/2T
None of these
The correct Answer is:B
Step by step video, text & image solution for A particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass m. They come in contact for a very small time t_0. Their force of interaction increases from zero to F_0 linearly in time 0.5t_0, and decreases linearly to zero in further time 0.5t_0 as shown in figure. The magnitude of F_0 is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion & Reason25videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test16videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Critical Thinking19videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise319videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)10videos
ROTATIONAL MOTION
Similar Questions
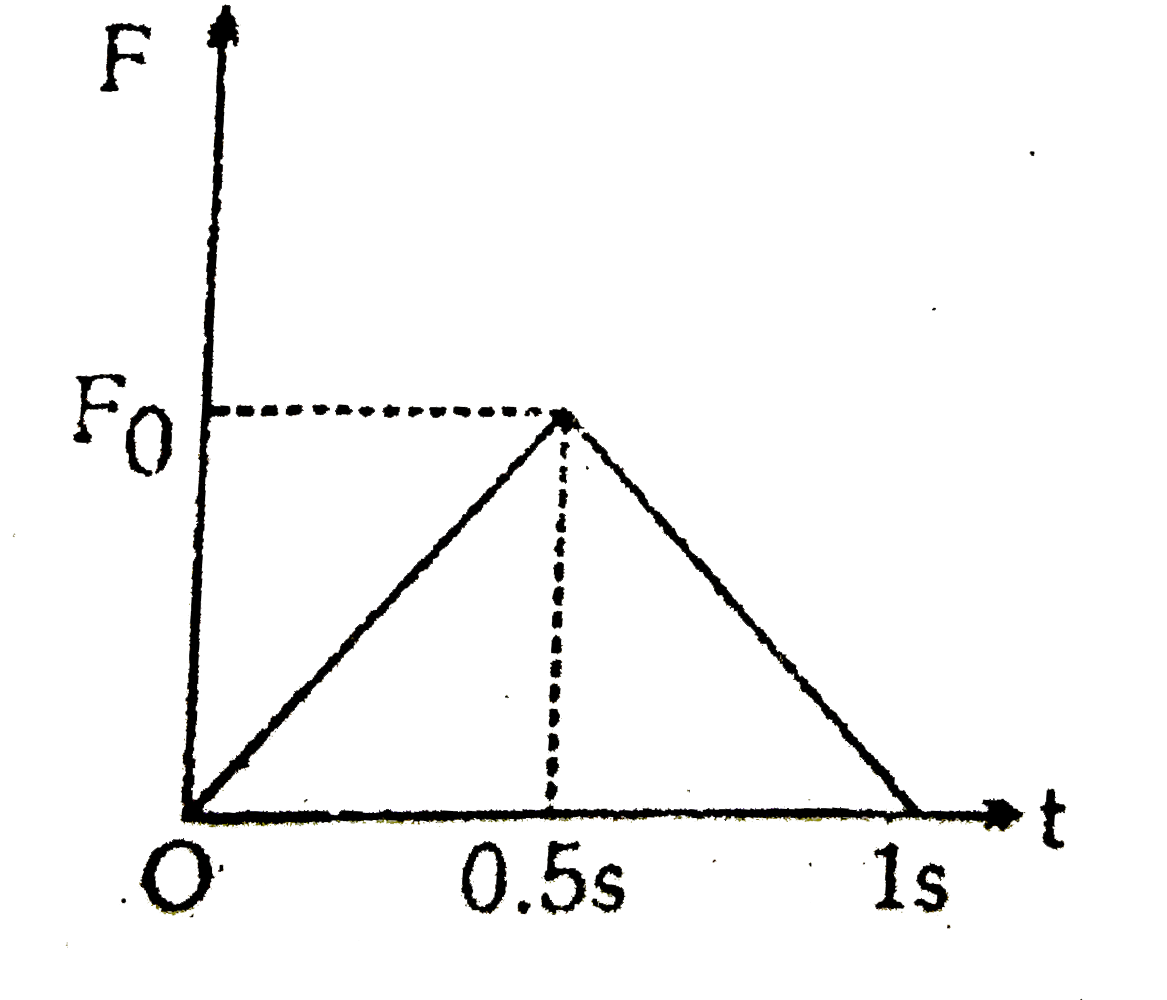
A body of mass 1kg moving with velocity 1ms makes an elastic one dimensional collision with an identical stationary body. They are in contact for brief time 1(~s). Their force of interaction increases from zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5s as shown in the figure. The magnitude of force F0 (in newton) is
'(##CEN_KSR_PHY_JEE_C08_E01_009_Q05##)'View SolutionA body of mass 1kg moving with velocity 1m/s makes an elastic one dimesional collision with an identical stationary body. They are in contact for brief time 1sec. Their force of interaction increases form zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5sec as shown in figure. Find the magnitude of force F0 in newton.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .AmuTB2muTC4mu3TD3mu4T
.AmuTB2muTC4mu3TD3mu4T - Question 2 - Select One
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2m - Question 3 - Select One
At t=0 aparticle of mass m start moving from rest due to a force →F=F0sin(ωt)ˆi :
AParticle perform SHM about its initial position of restBParticle perform SHM with initial position as extreme position with angular frequency ωCAt any instant, distance moved by the particle equals its displacement, from the initial positionDinitial velocity of particle increases with time but after time t=2π/ω it becomes constant
A particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the
 View Solution
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.
 View Solution
View SolutionFind the time t0 when x-coordinate of the particle is zero.
View SolutionThe velocity of a particle is zero at t=0
View SolutionA particle of rest mass m0 starts moving at a moment t=0 due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.
View Solution

