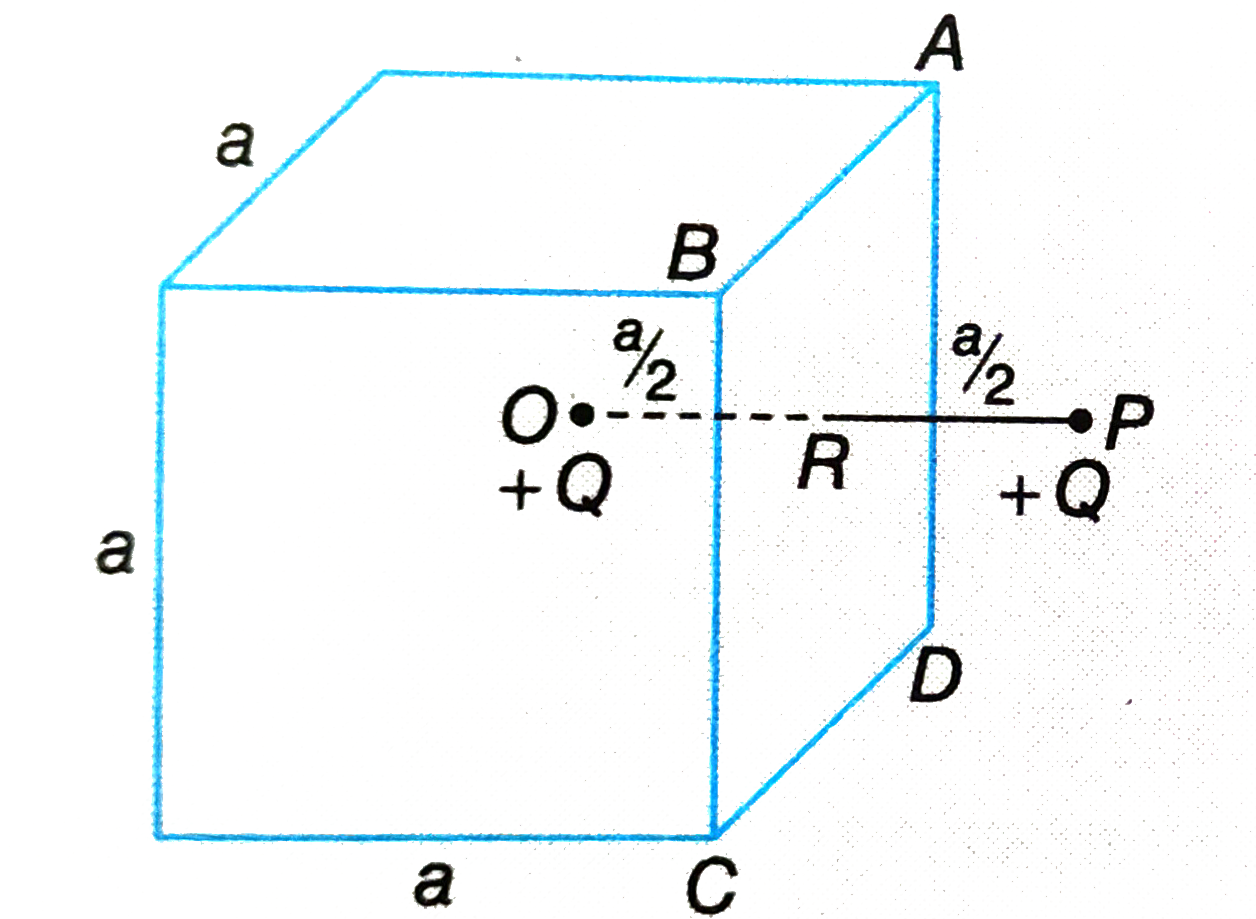
Consider a region in free space bounded by the surfaces of an imaginary cube having sides of length a as shown in the diagram. A charge +Q is placed at the centre O of the cube. P is such a point outside the cube that the line OP perpendicularly intersects the surface ABCD at R and also $O R = R P = \frac{a}{2}$ . A charge +Q is placed at point P also. What is the total electrie flux through the five faces of the cube other than ABCD?

$\frac{Q}{\in_{0}}$

$\frac{5 Q}{6 \in_{0}}$

$\frac{10 Q}{6 \in_{0}}$

zero

Text Solution

Verified by Experts

According to Gauss' theorem,
$ϕ = \oint_{s} \to E . d \to s = \frac{Q}{\in_{0}}$
The electric flux linked with each surface of the cube are equal and is given by,
$ϕ = \frac{Q}{6 \in_{0}}$
The total electric flux linked with the five faces of the cube other than ABCD due to charge +Q at point O is $\frac{5 Q}{6 \in_{0}}$ . Given, $O R = R P = \frac{a}{2}$ and the charges placed at points P and Q are equal.
Now, if the charge +Q placed at point P is enclosed by a similar cube, then the electric flux only through surface ABCD will be $\frac{Q}{6 \in_{0}}$ . The same amount of flux $(\frac{Q}{6 \in_{0}})$ will emerge from the remaining five surfaces of the cube centred at O.
Hence the total electric flux linked with the five faces other than ABCD
$= \frac{5 Q}{6 \in_{0}} + \frac{Q}{6 \in_{0}} = \frac{Q}{\in_{0}}$
The optino (A) is correct.

Updated on:21/07/2023