A particle with charge QC, tied at the end of an inextensible string of length R metre, revolves in a vertical plane. At the centre of the circular trajectory there is a fxied charge of magnitude QC. The mass of the moving charge M is such that Mg=Q24πε0R2 . If at the highest position of the particle, the tenstion of the string just vanishes, the horizontal velocity at the lowest point has to be Solution in Bengali
0
2√gR
√gR
√5gR
From the figure 2.116, tension on the top of vertuicle circular path is zero.
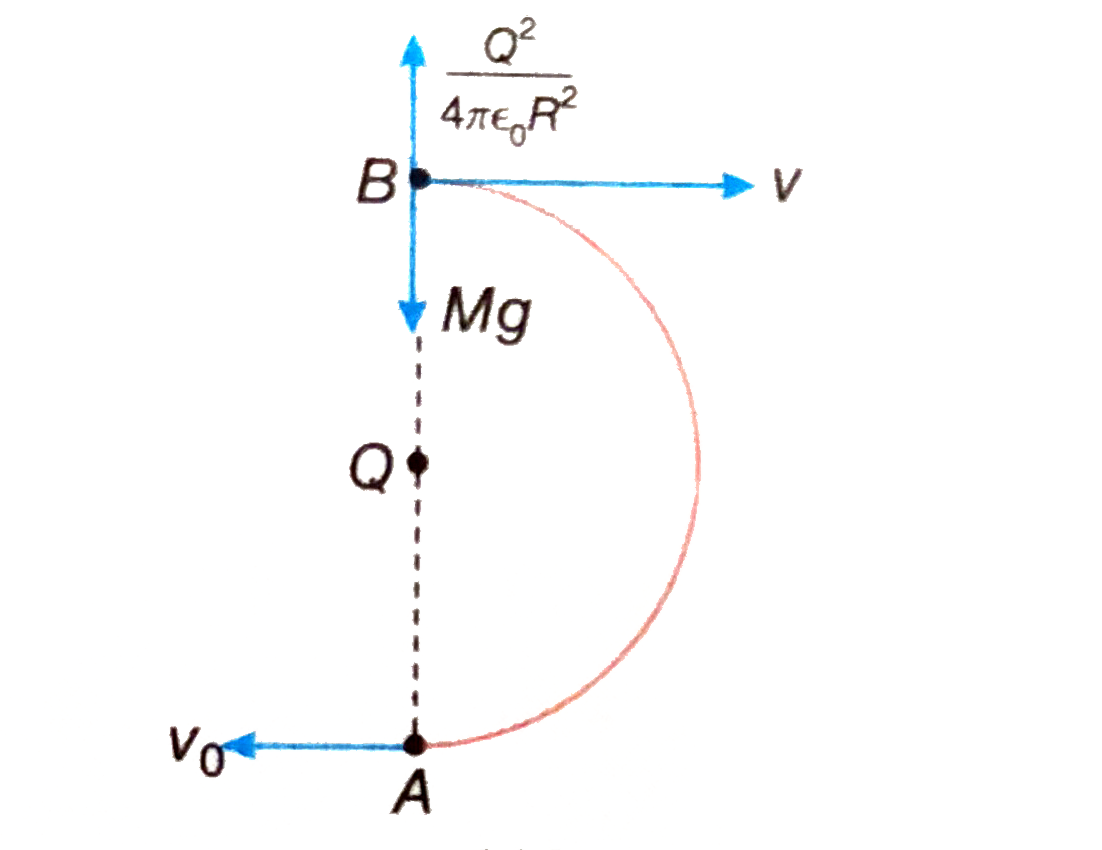
Therefore, at that position,
Mg−Q24πε0R2=Mv2R
But Mg−Q24πε0R2
∴v=0
Now, from the conservation of mechanical energy,
(PE)B=(ΔKE)A[∴(KE)B=12Mv2=0]
or, Mg×2R=1RMv20or,v0=2√gR
The option (B) is correct.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( JEE MAIN )3videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( AIPMT)1videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE (WBCHSE)13videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER7videos
ELECTRIC ENERGY AND POWER
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner13videos
ELECTRIC POTENTIAL
Similar Questions
A long cylindrical shell carries positive surface charge σ in the upper half and negative surface charge −σ in the lower half. The electric field lines around the cylinder will look like figure given in (figures are schematic and not drawn to scale)
05:50View SolutionThe eletric field in a certina region is acting radially outward and is given by E = Ar. A charge contained in 'a' centred at the origin of the field will be givne by
View SolutionFour point charges +q,+q,+q and −q are placed at the four comers of a square, length of each side of which is a.
Find the magnitude of the intensity of the electric field at the centre of the square.View SolutionA light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate
the resistance of the bulb ,04:45View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.03:39View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
01:58View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q = 1muC , mass of each particle m=6g . The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface. What is the tension in the string?
12:18View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q = 1muC , mass of each particle m=6g . The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface. Now suppose a third charge of equal value +q is fixed at the point (a//2,0) and the system of charges A and B is released. There is no friction between third charge and string. Find the maximum velocity of the system of charges A and B.
05:09View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q = 1muC , mass of each particle m=6g . The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface. What is the tension in the string when velocity is maximum.
04:57View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u = sqrt((5)/(2)gl) The tension in the string at an instant when acceleration of the particle is horizontal and sqrt(3)g is
03:55View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
05:54View SolutionA heavy particle is tied to the end A of a string of the length 1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60^(@) with the horizontal. Then,
06:49View SolutionA particle with charge Q coulomb, tied at the end of an inextensible string of length R metre, revolves in a vertical plane. At the centre of the circular trajectory, there is a fixed charge of magnitude Q coulomb . The mass of the moving charge M is such that Mg=Q^2/(4pivarepsilon_0R^2) . If at the highest position of the particle, the tension of the string just vanishes, the horizontal velocity at the lowest point has to be
03:08View SolutionA charged particle of mass m1 and charge q1 is revolving in a circle of radius r .Another charged particle of charge q2 and mass m2 is situated at the centre of the circle.If the velocity and time period of the revolving particle be v and T respectively then
05:41View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v_( 0) to complete the vertical circle. The tension in the string when it becomes horizontal is
07:36View Solution

