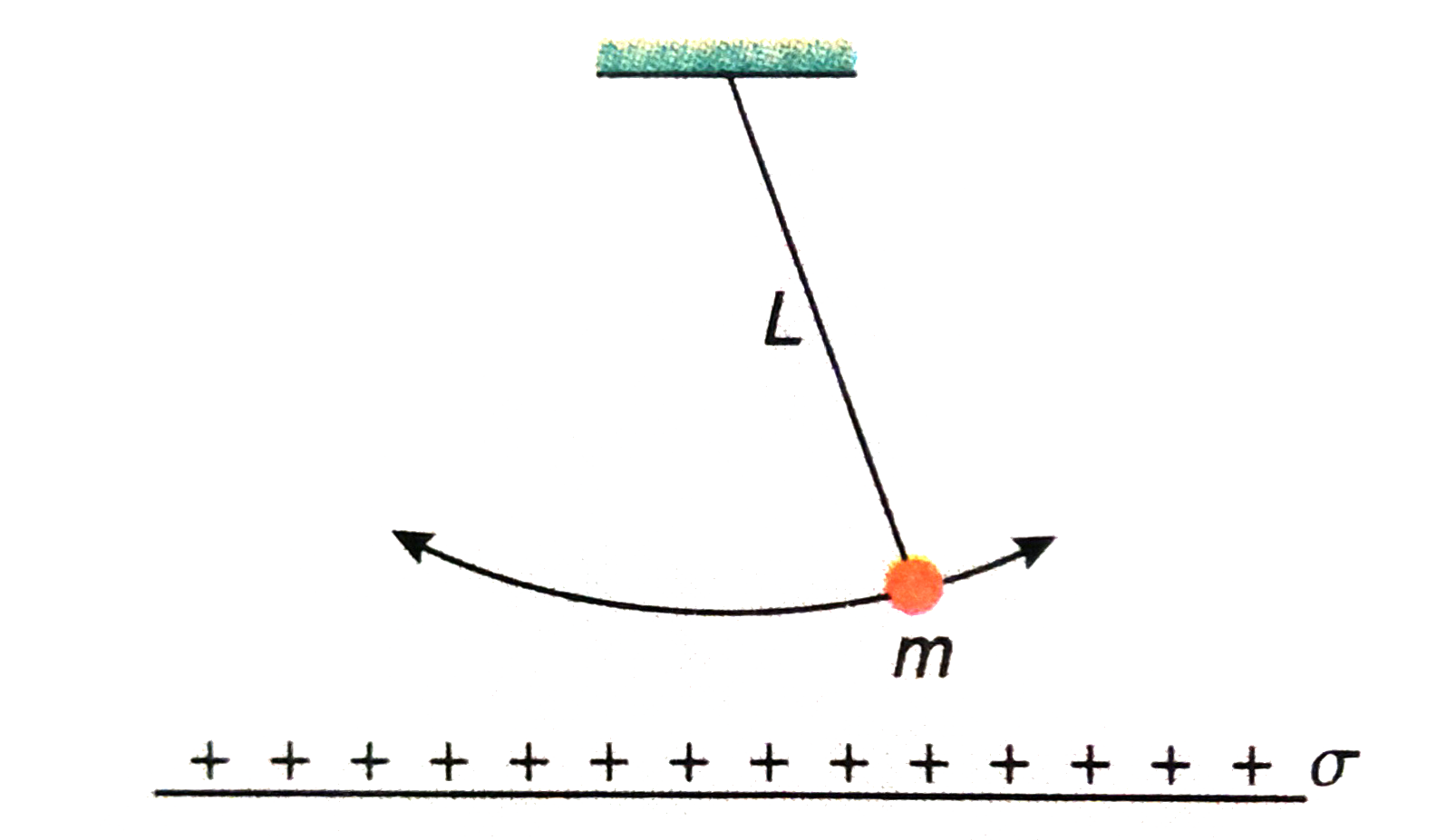
The bob of a pendulum of mass m, suspended by an inextensible string of length L as shown in the figure carries a small charge q. An infinite horizonatal plane conductor with uniform surface charge density σ is placed below it. What will be the time period of the pendulum for small amplitude oscillations?
2π ⎷L(g−qσ∈0m)
⎷L(g−mqσ∈0)
12π ⎷L(g−qσ∈0m)
2π ⎷L(g−qσ∈0m)
Electric field due to a conducting plate, E=σ∈0
Electric force on the bob of the pendulum, Fe=qE=qσ∈0
The force Fe is directed opposite to gravity.
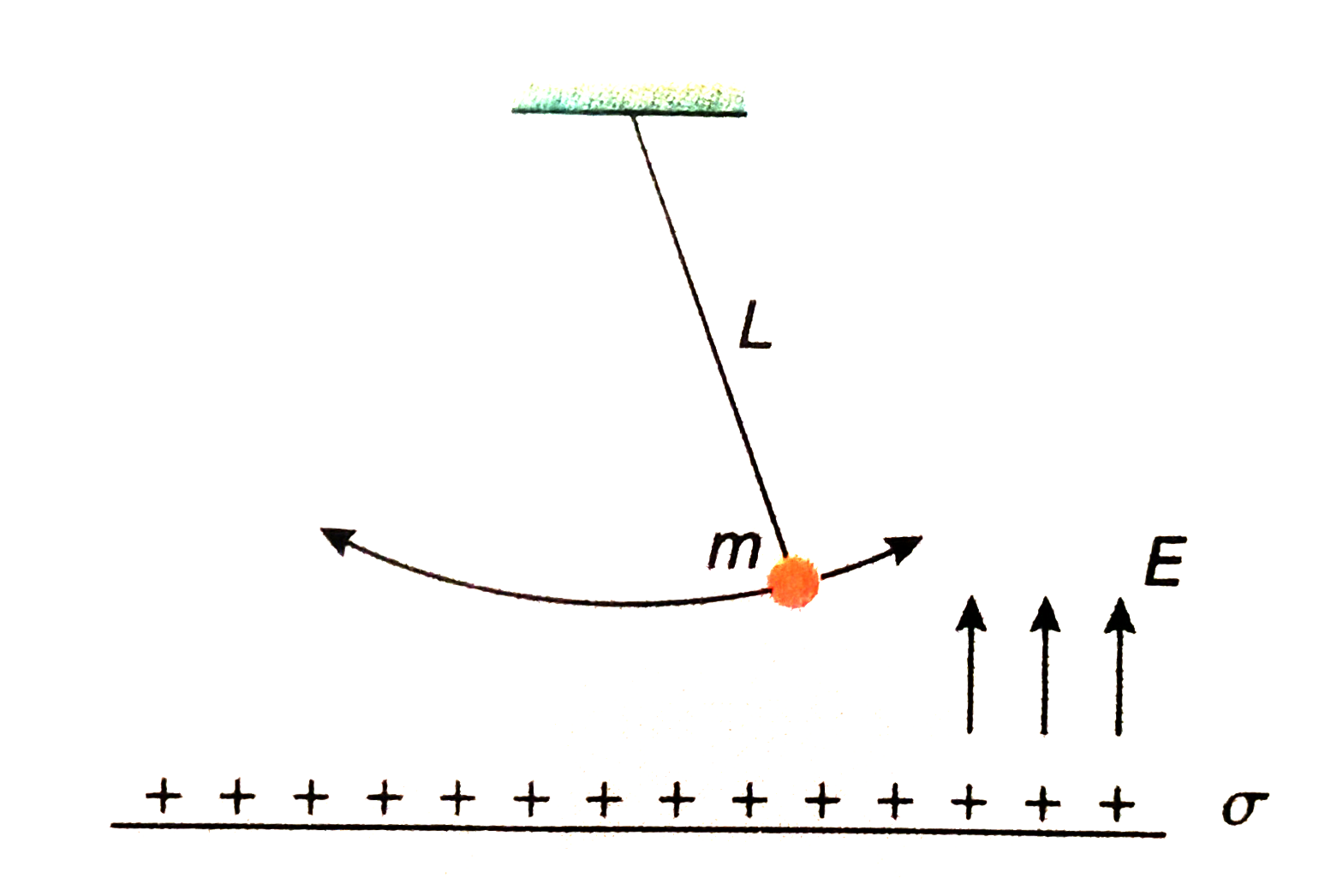
The net force on the bob directed vertically downwards,
F'mg'=mg=Fe=m(g−qσ∈0m)
or, g'=g−qσ∈0m
∴ Time period for small amplitude oscillations,
T=2π√Lg'=2π
⎷L(g−qσ∈0m) .
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( JEE MAIN )
3 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( AIPMT)
1 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE (WBCHSE)
13 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
A bob of a simple pendulum of length l is negatively charged. A positively-charged metal plate is placed just below the bobt and the pendulum is made to oscillate. What will be the effect on the time period of the pendulum?
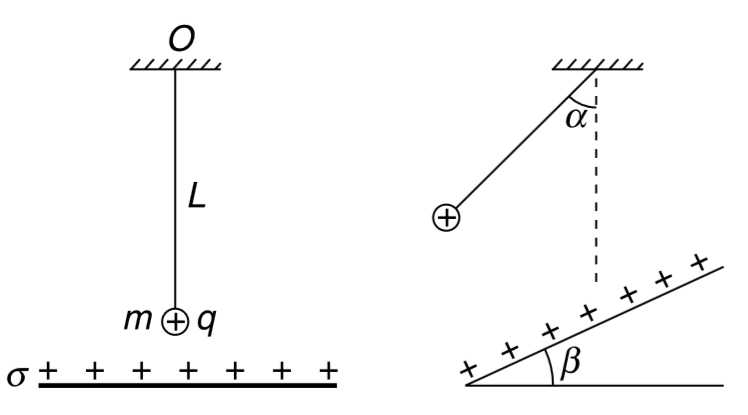
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View Solution
Knowledge Check
Consider a parallel plate capacitor having an electric field E inside it as shown in the adjacent figure. A particle of mass m and charge q is hanging inside the capacitor through a light inextensible string of length. The time period of this pendulum of small oscillations is
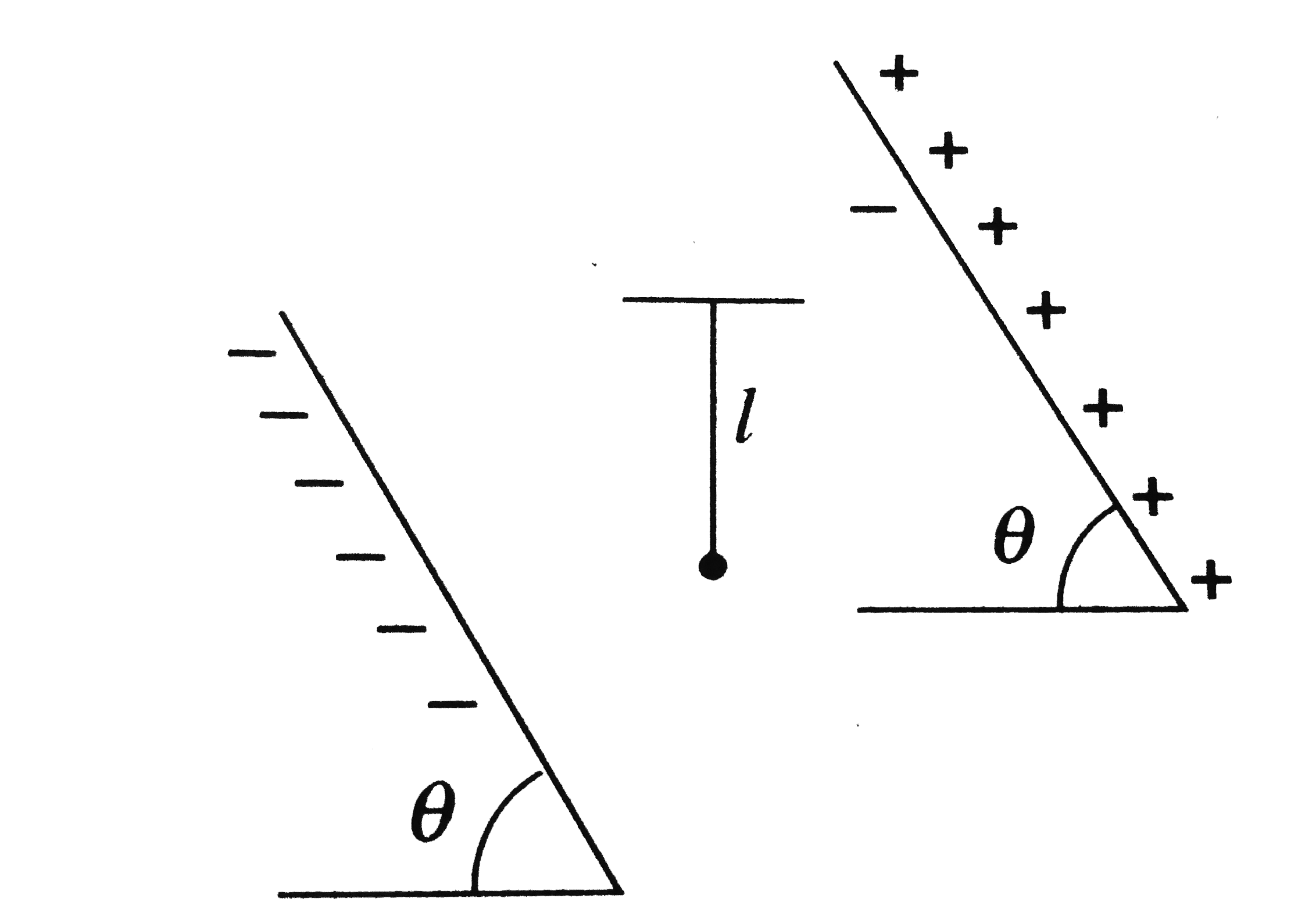 AT=2π√lg+(qE/m)BT=2π ⎷l√g2+q2E2m2−2qgEmCT=2π ⎷l√g2+q2E2m2+2qgEmDnone of these
AT=2π√lg+(qE/m)BT=2π ⎷l√g2+q2E2m2−2qgEmCT=2π ⎷l√g2+q2E2m2+2qgEmDnone of theseA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a verticle plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the verticle can be
A90∘B60∘C30∘D0∘
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force?
View SolutionThe bob of a simple pendulum is positively charged. A negatively charged metal plate is placed just below the bob as the pendulum starts oscillating. How will it affect the time period of the pendulum?
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Finds the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
View SolutionA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a vertical plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the vertical can be
View Solution
