It the point charge is now moved to a distance d from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected. Solution in Bengali
If the distance of the point charge from the centre of the square is now doubled, the side of the square also gets doubled. So from the same symmetry, the flux through the square will still be q6ε0.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( NEET )4videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER7videos
ELECTRIC ENERGY AND POWER
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner13videos
ELECTRIC POTENTIAL
Similar Questions
Two identical charged spheres suspended from a common point by two masses strings of length l are initially at a distance d (d lt lt 1) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charge approaches each other with a velocity v. Then as a function of distance x between them
02:48View SolutionA light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate
the resistance of the bulb ,01:17View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.03:27View SolutionA point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
04:59View Solution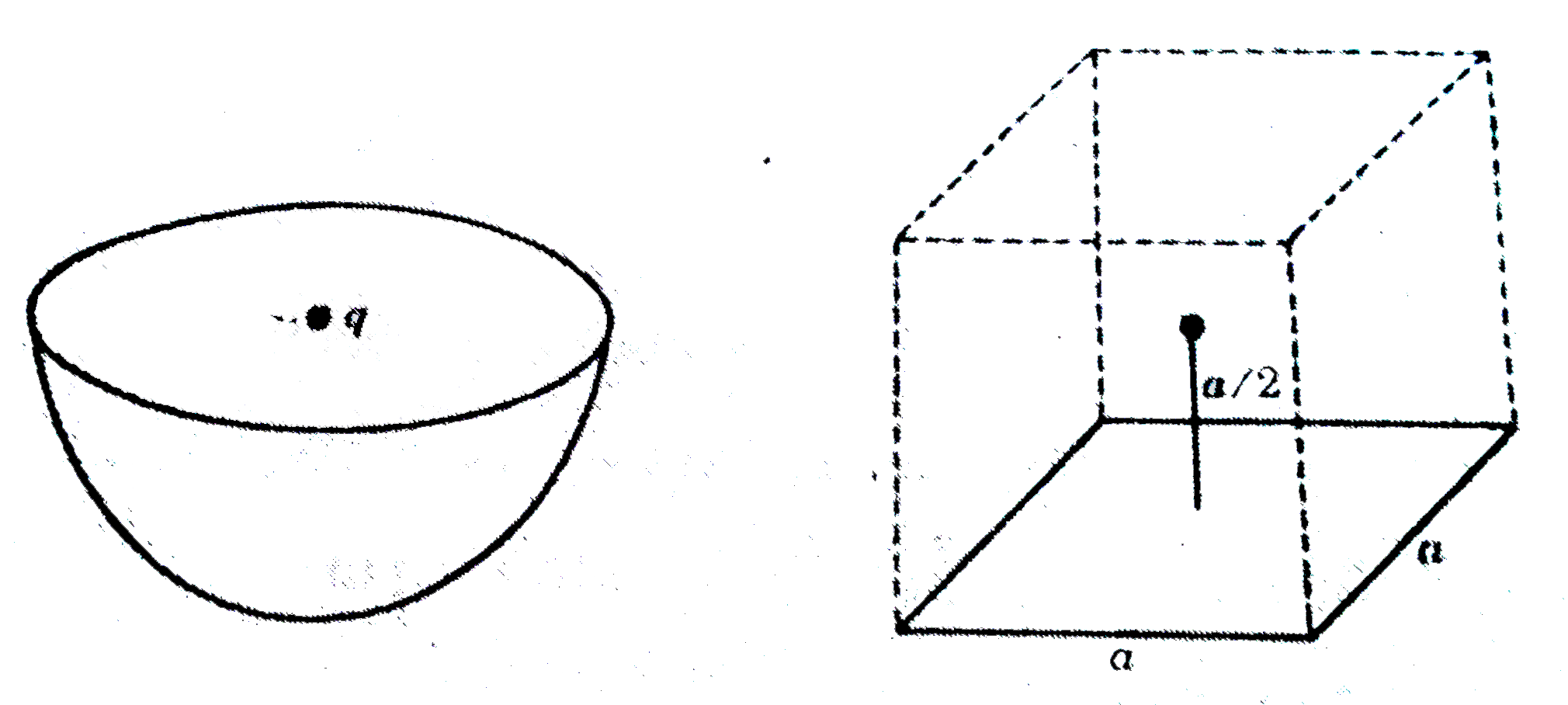
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.06:50View Solution(a) Define electric flux. Is is the scalar or a vector quantity?
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss's law to obtain the expression for the electric flux through the square.
(b) If the point charges is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.
 10:03View Solution
10:03View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
02:08View SolutionA point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
05:15View SolutionA point charge q is placed at a distance (a)/(2) directly above the centre of a horizontal square of side 'a' and another point charge -q is placed at a distance 'a' directly below one of its (the square's) corners. The electric flux through the square is :
02:56View SolutionA point charge of +6mu C is placed at a distance 20 cm directly above the centre of a square of side 40 cm. The magnitude of the flux through the square is
06:50View SolutionIf the point charge is now moved to a distance 'd' form the centre of the square and the side of the square is doubled explain how the electric flux will be affected.
02:49View SolutionA point charge Q is kept at the centre of a square face of edge length a. The amount of electric flux associated with the square face in
View SolutionA point charge + mu c is a distance 5 cm directly above the centre of a square of side 10 cm as what is the magnitude of the electric flux through the square
02:11View SolutionA point charge + mu c is a distance 5 cm directly above the centre of a square of side 10 cm as what is the magnitude of the electric flux through the square
01:44View SolutionDefine electric flux, Is it a scalar or a vector quantity? A point charg q is at a distance of d2 directly above the centre of a square of side 'd' Use Gauss' law to obtain the expression for the electric flux through the square.
(b) If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled , explain how the electric flux will be affected.06:50View Solution

