A particle of mass $m = 2 k g$ executes $S H M$ in $x y$ - plane between point A and B under action of force $\to F = F_{x} ˆ i + F_{y} ˆ j$ . Minimum time taken by particle to move from A to B is 1 sec. At $t = 0$ the particle is at $x = 2$ and $y = 2$ . Then $F_{x}$ as function of time t is

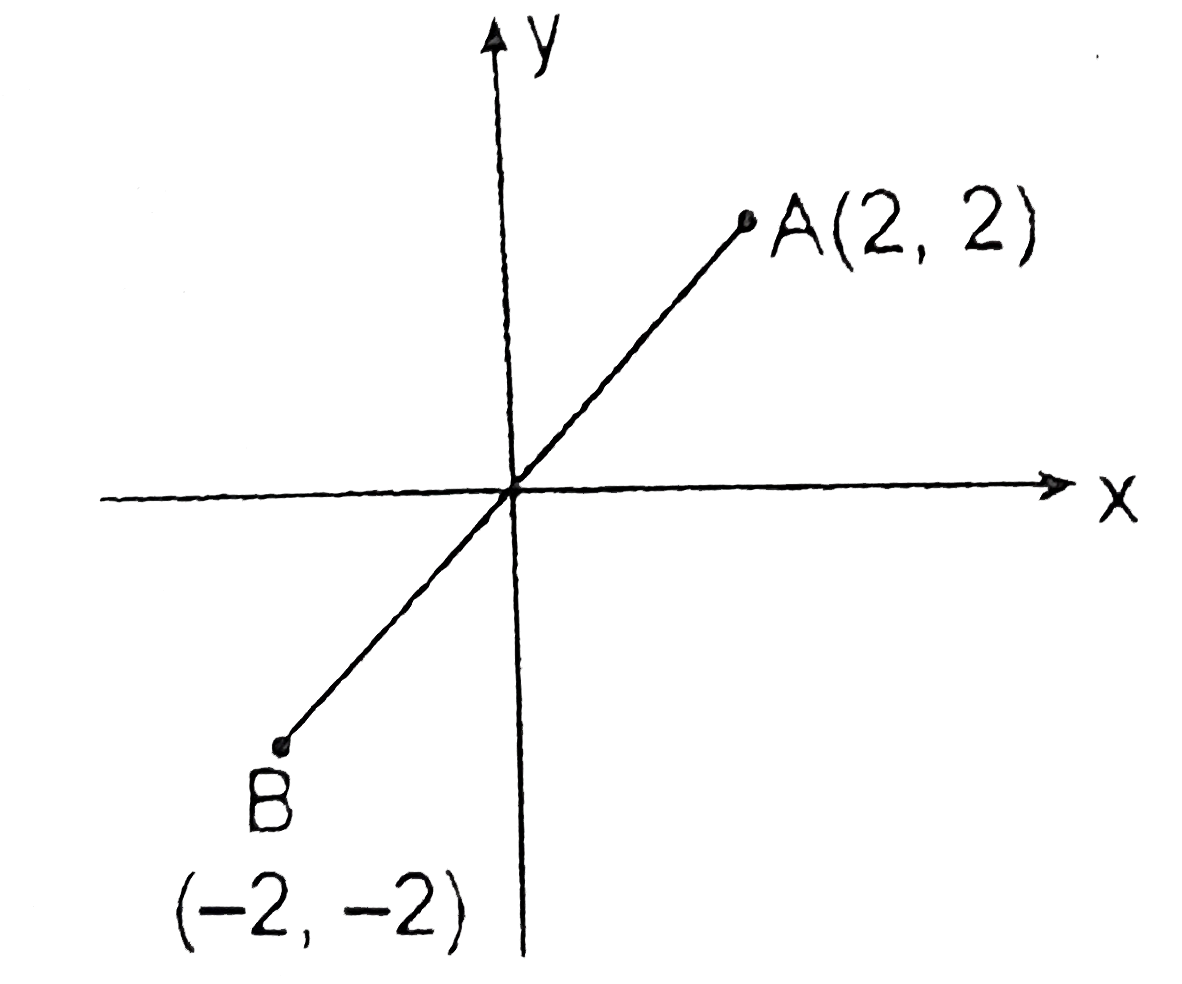
$- 4 π^{2} sin π t$

$- 4 π^{2} cos π t$

$4 π^{2} cos π t$

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for A particle of mass m = 2kg executes SHM in xy- plane between point A and B under action of force vecF = F_(x)hati+F_(y)hatj. Minimum time taken by particle to move from A to B is 1 sec. At t = 0 the particle is at x = 2 and y = 2. Then F_(x) as function of time t is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A particle of mass $2 k g$ moves in the $x y$ plane under the action of a constant force $\to F$ where $\to F = ˆ i - ˆ j$ . Initially the velocity of the particle is $2 ˆ j$ . The velocity of the particle at time $t$ is
A $\frac{1}{2} (t + 4) ˆ i - \frac{1}{2} t ˆ j$
B $t (ˆ i - ˆ j)$
C $\frac{1}{2} t (ˆ i - ˆ j)$
D $\frac{1}{2} t ˆ i + \frac{1}{2} (t + 4) ˆ j$
Question 2 - Select One
Particle moves from point A to point B along the line shown in figure under the action of force. $e v c F = - x ˆ i + y ˆ j$ . Determine the work done on the particle by $\to F$ in moving the particle from point A to point B.
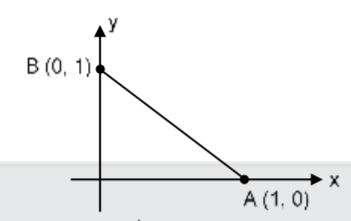A1 J
B1/2 J
C2 J
D3 J
Question 3 - Select One
A particle of mass m moves from A to C under the action of force $\to F = 2 x y ˆ i + y^{2} ˆ j$ , along different paths as shown in figure.

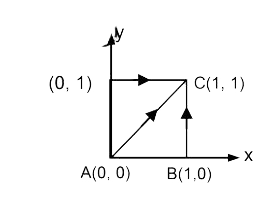AForce is conservative in nature
BWork done by force is $\frac{1}{3}$ when particle moves along path ABC
CForce is non conservative in nature and work done along path AC is 1 J
DWork done along path ADC is $\frac{14}{5} J$

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct Answer type

Home
Ask Doubt
Profile

A particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is

Particle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.

A particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct Answer type

A particle of mass $m = 2 k g$ executes $S H M$ in $x y$ - plane between point A and B under action of force $\to F = F_{x} ˆ i + F_{y} ˆ j$ . Minimum time taken by particle to move from A to B is 1 sec. At $t = 0$ the particle is at $x = 2$ and $y = 2$ . Then $F_{x}$ as function of time t is

A particle of mass $2 k g$ moves in the $x y$ plane under the action of a constant force $\to F$ where $\to F = ˆ i - ˆ j$ . Initially the velocity of the particle is $2 ˆ j$ . The velocity of the particle at time $t$ is

Particle moves from point A to point B along the line shown in figure under the action of force. $e v c F = - x ˆ i + y ˆ j$ . Determine the work done on the particle by $\to F$ in moving the particle from point A to point B.

A particle of mass m moves from A to C under the action of force $\to F = 2 x y ˆ i + y^{2} ˆ j$ , along different paths as shown in figure.