A particle of mass m is subjected to a force →F=F0[cos(t)ˆi+sin(1)ˆj]. If initially (t=0) the particle was at rest, the kinetic energy of the particle as a function of time is given by:
F20m(1−cos(2t))
F20m(1−cost)
F20msin(t)
F20mt
→a=→Fm=F0m[cos(t)ˆi+sin(t)ˆj]
→v=∫t0→adt=F0m[sin(t)ˆi+(1−cost)ˆj]
KE=12m(→v.→v)=12m[F20m2(2−2cost)]
=F20m(1−cost)
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A particle of unknown mass is acted upon by a force →F=(100e−2tˆi)N. If at t = 0.00 s the particle is at rest, for the time interval t=0.00 s to t= 2.00 s find (a) the impulse on the particle and (b) the average force on the particle.
View SolutionA particle of mass m kept at the origin is subjected to a froce →F=(pt−qx)ˆi where t is the time elapsed and x is the x co-ordinate of the position of the particle. Particle starts its motion at t=0 with zero initial velocity. If p and q are positive constants, then:
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is released from rest and follows a particle as a function of time?
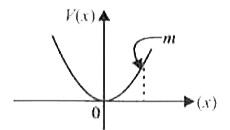 A
A B
B C
C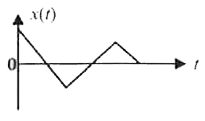 D
D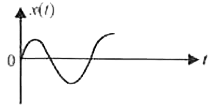
- Question 2 - Select One
At t=0 aparticle of mass m start moving from rest due to a force →F=F0sin(ωt)ˆi :
AParticle perform SHM about its initial position of restBParticle perform SHM with initial position as extreme position with angular frequency ωCAt any instant, distance moved by the particle equals its displacement, from the initial positionDinitial velocity of particle increases with time but after time t=2π/ω it becomes constant - Question 3 - Select One
A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
Aits displacement will be in simple harmonicBits velocity will be in simple harmonicCits acceleration will be in simple harmonicDNone of the above
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionFor a particle moving on a straight lint the variation of acceleration with time is given by the graph as shown. Initially the particle was at rest. Then the corresponding kinetic energy of the particle versus time graph will be
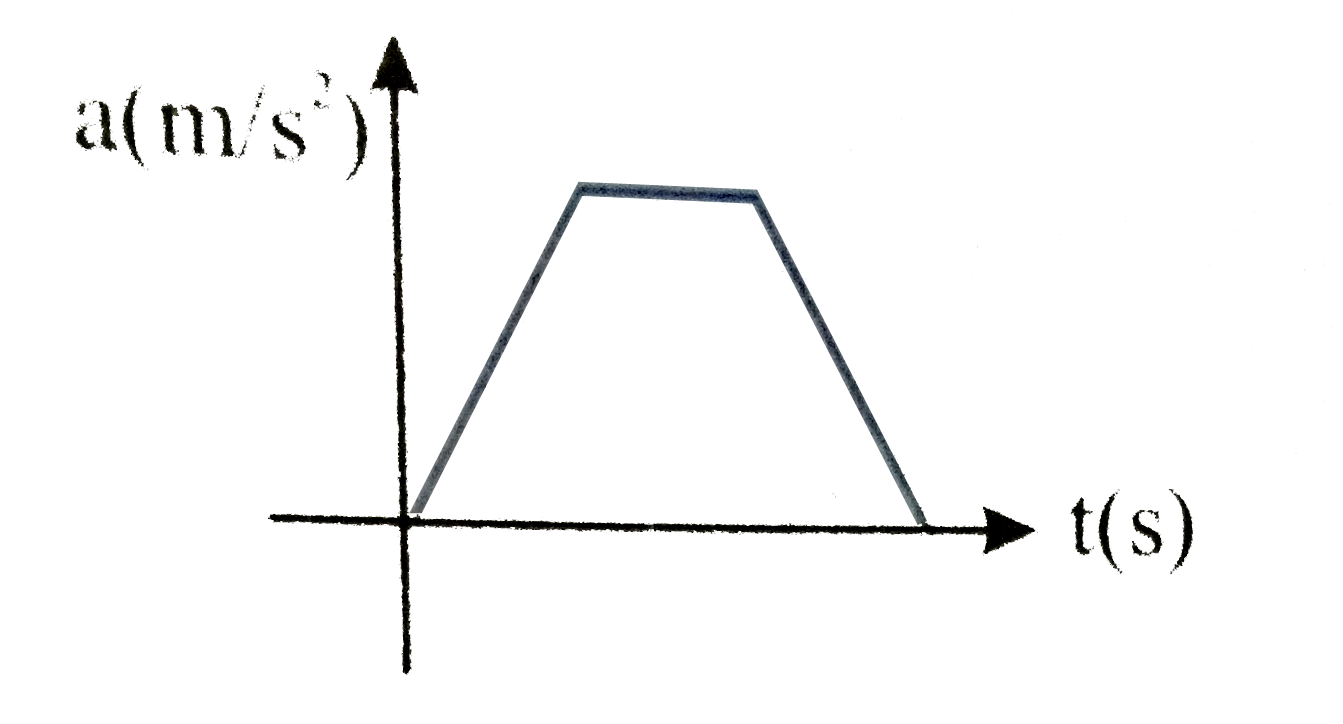 .View Solution
.View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View Solution

