The moments of inertia of a non-uniform circular disc (of mass M and radius R) about four mutually perpendicular tangents AB, BC, CD, DA are I1,I2,I3 and I4, respectively (the square ABCD circumscribes the circle). The distance of the center of mass of the disc from its geometrical center is given by -
14MR√(I1−I3)2+(I2−I4)2
112MR√(I1−I3)2+(I2−I4)2
13MR√(I1−I2)2+(I3−I4)2
12MR√(I1+I3)2+(I2+I4)2
The correct Answer is:A
Step by step video, text & image solution for The moments of inertia of a non-uniform circular disc (of mass M and radius R) about four mutually perpendicular tangents AB, BC, CD, DA are I_(1), I_(2), I_(3) and I_(4), respectively (the square ABCD circumscribes the circle). The distance of the center of mass of the disc from its geometrical center is given by - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
 05:53View Solution
05:53View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
01:41View SolutionLet I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
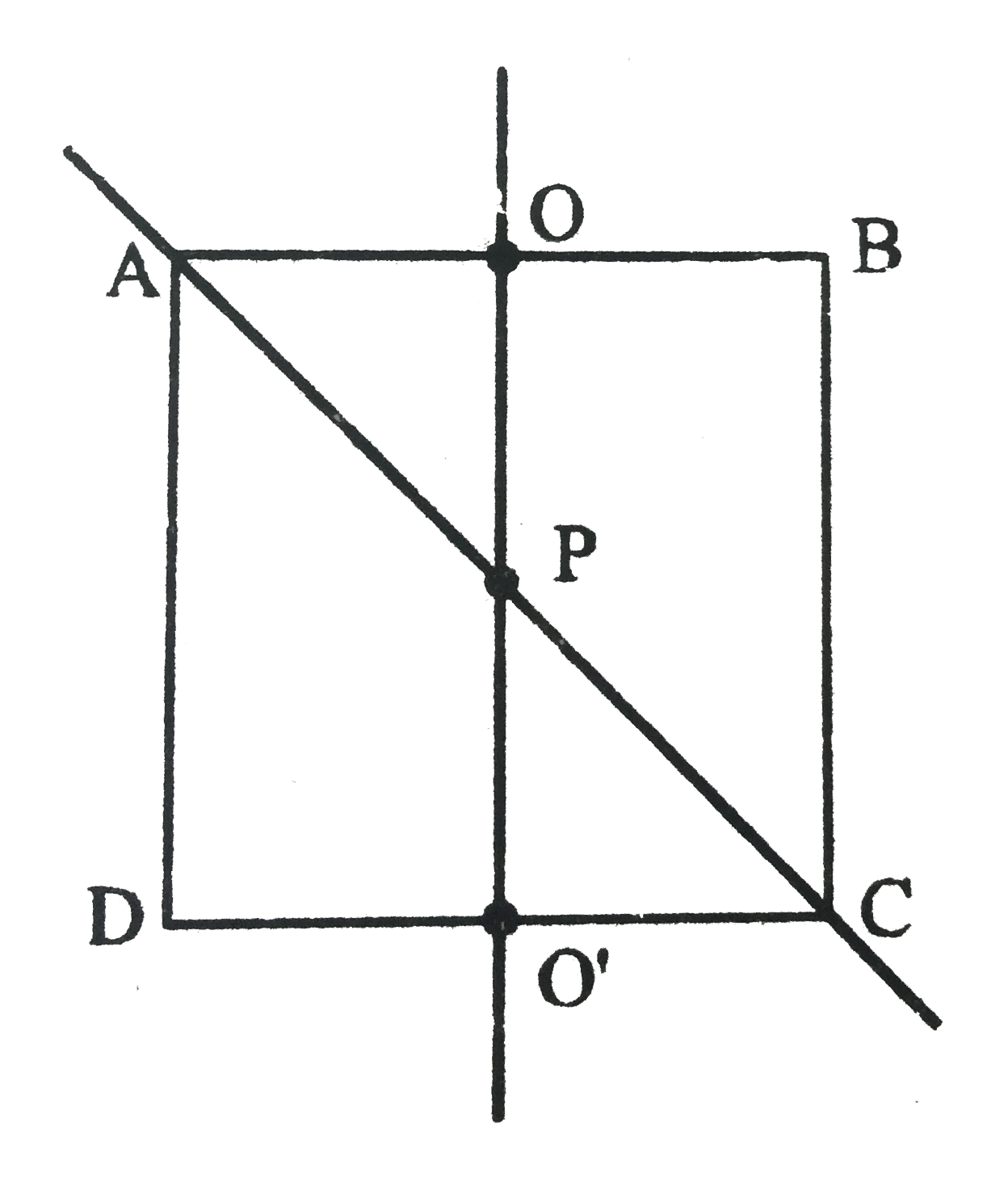 .01:18View Solution
.01:18View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
03:42View SolutionThe moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is ( i ) I_(1)+I_(2) ( ii ) I_(2)+I_(4) ( iii ) I_(1)+I_(3) ( iv ) I_(1)+I_(2)+I_(3)+I_(4) where I_(1) , I_(2) , I_(3) and I_(4) are repectively moments of inertia about axes 1 , 2 , 3 and 4 which are in the plane of the plane
04:32View SolutionA solid sphere of mass M and radius R is divided into two unequal parts. The first part has a mass of (7M)/(8) and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let I_(1) be the moment of inertia of the disc about its axis and I_(2) be the moment of inertia of the new sphere about its axis. The ratio (I_(1))/(I_(2)) is equal to __________ .
03:56View Solutionएक समान मोटाई की एक पतली वर्गाकार प्लेट ABCD का प्लेट के तल के लम्बवत तथा उसके केंद्र O से जाने वाली अक्ष के परितः जड़त्व आघूर्ण होगा
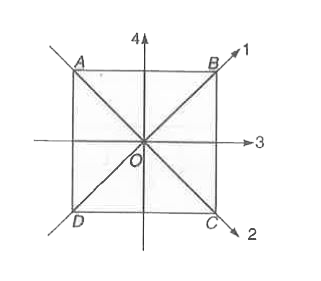
जहां I1,I2,I3 तथा I4 क्रमशः 1,2,3 तथा 4 प्लेट के तल में स्थित अक्षों के परितः जड़त्व आघूर्ण हैं03:02View SolutionIf I_(1) , I_(2) ,and I_(3) are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then
07:07View SolutionA solid sphere of mass M and radius R is divided into two unequal parts. The first parts has a mass of 7M8 and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let I1 be the moment of inertia of the uniform disc about its axis and I2 be the moment of inertia of the sphere made from remaining part about its axis. The ratio I1/I2 is 140x. Find the value of x.
04:29View SolutionM द्रव्यमान तथा R त्रिज्या की वृत्तीय चकती का द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण I0 है। एक अन्य समान द्रव्यमान तथा मोटाई किन्तु आधे घनत्व की वृत्तीय चकती का उसी अक्ष के परितः जड़त्व आघूर्ण होगा
04:52View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
04:52View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
05:55View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
05:33View SolutionIf I_(1)I_(2) , and I_(3) are moments of inertia of a disc about its geometric axis, diameter and a tangent in its plane, then
View SolutionIf I1,I2 and I are moments of inertia of a disc about its geometric axis, diameter and a tangent in its plane, then
05:33View Solution

