The pendulum on a clock swings through an angle of 1 radian, and the tip sweeps out ann arc of 12 inches. How long is the pendulum?
3.8 inches
6 inches
7.6 inches
12 inches
The correct Answer is:D
To find the length of the pendulum, we can use the relationship between the angle in radians, the arc length, and the radius (which in this case is the length of the pendulum). The formula we will use is:
Angle (in radians)=Arc LengthRadius
Given:
- The angle θ=1 radian
- The arc length s=12 inches
We need to find the radius (length of the pendulum), denoted as L.
1. Write the formula:
θ=sL
2. Substitute the known values into the formula:
1=12L
3. Rearrange the equation to solve for L:
L=121
4. Calculate L:
L=12 inches
Thus, the length of the pendulum is 12 inches.
- The angle θ=1 radian
- The arc length s=12 inches
θ=sL
1=12L
L=121
L=12 inches
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
the pendulum on a clock swings through an angle 25∘, and the tip sweeps out an arc of 12 inches. How long is the pendulum?
A1.67 inchesB13.8 inchesC27.5 inchesD43.2 inches - Question 2 - Select One
The bottom of a pendulum traces an arc 3 feet in length when the pendulum swings through an angle of 12 radians.What is the number of feet in the length of the pendulum?
A1.5B6C1.5πD6π
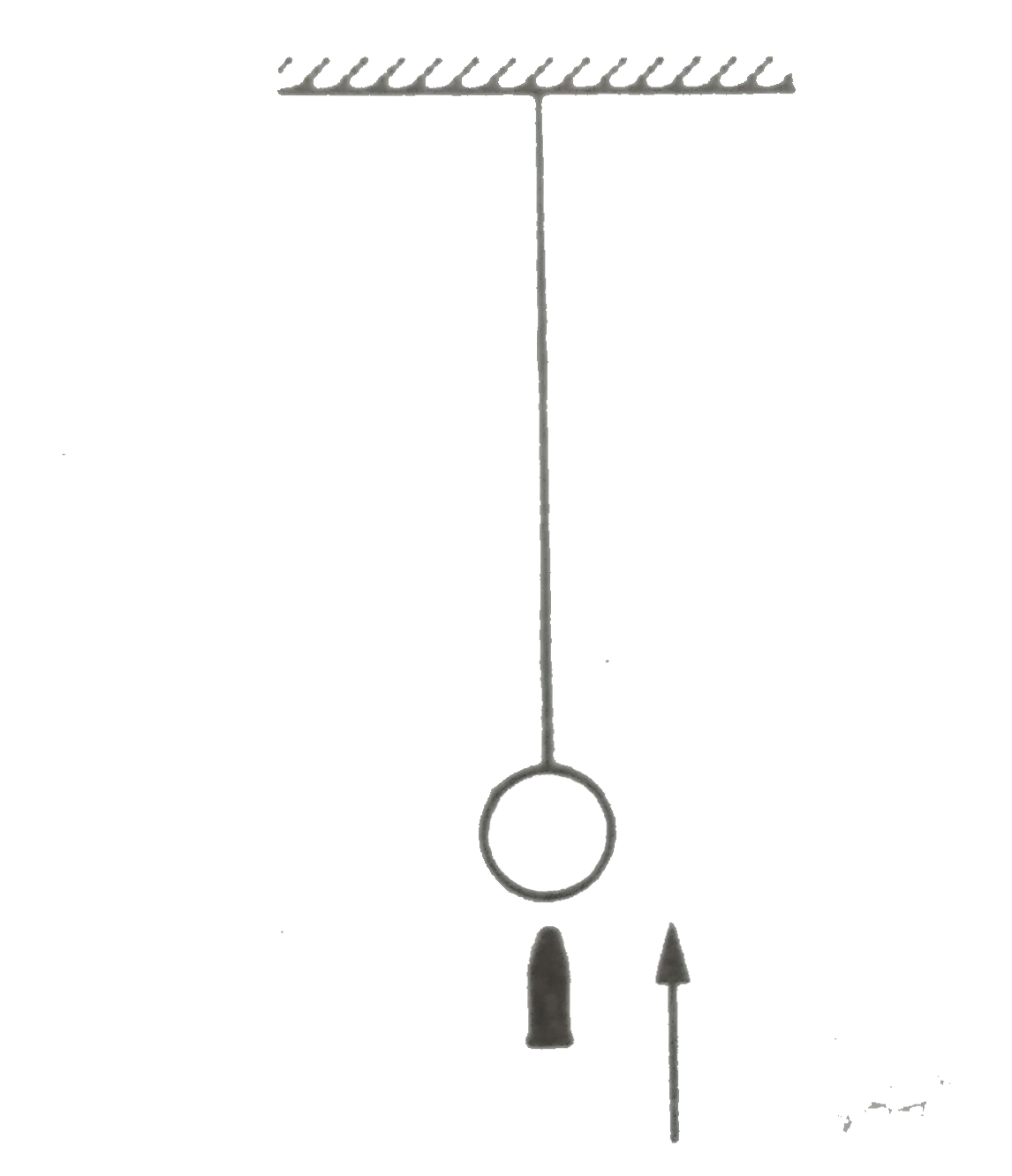
A bullet of mass 50g if fired from below into the bob of mass 450g of a long simple pendulum as shown in Fig. The bullet remains inside the bob and the bob rises through a height of 1.8m. Find the speed of the bullet.Take g=10ms2
 View Solution
View SolutionA certain pendulum clock with a 12 hr dial happens to gain 1 min/day. After setting the clock to the correct time how long it will take to indicate correct time again?
View SolutionA pendulum has a period T for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.
 View Solution
View SolutionFind the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length (i) 10 cm (ii) 15 cm (iii) 21 cm
View SolutionFind the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length (i) 10 cm (ii) 15 cm (iii) 21 cm
View SolutionFind the angle in radian through which a pendulum swings if its length is 75cm and the tip describes an arc of length: 15cm(useπ=227)
View Solution

