In the accompanying diagram of triangle ABC, AC=BC, D is point on ¯¯¯¯¯¯AC,¯¯¯¯¯¯AB is extended to E, and ¯¯¯¯¯¯¯¯¯DEF is drawn so that △ADE−△ABC. If m∠C=30, what is the value of x?
The correct Answer is:45
To solve the problem step by step, let's follow the reasoning based on the information provided in the question and the video transcript.
Step 1: Understand the properties of triangle ABC
Since AC = BC, triangle ABC is an isosceles triangle. This means that the base angles are equal. Given that angle C = 30°, we can find the other two angles.
Hint: Recall that the sum of angles in a triangle is 180°.
Step 2: Calculate the base angles of triangle ABC
Let the base angles be denoted as angle A and angle B. Since AC = BC, we have:
angle A=angle B
Using the triangle angle sum property:
angle A+angle B+angle C=180°
Substituting the known value:
angle A+angle A+30°=180°
This simplifies to:
2×angle A+30°=180°
Hint: Isolate the variable to find the value of angle A.
Step 3: Solve for angle A
Subtract 30° from both sides:
2×angle A=180°−30°
2×angle A=150°
Now divide both sides by 2:
angle A=75°
Hint: Remember that since angle A and angle B are equal, they both have the same measure.
Step 4: Establish the relationship between triangles ADE and ABC
Since triangle ADE is similar to triangle ABC (as stated in the problem), the corresponding angles are equal. Therefore:
angle C=angle E
Thus:
angle E=30°
Hint: Use the property of similar triangles that states corresponding angles are equal.
Step 5: Relate angle X to the angles in triangle ADE
In triangle ADE, we know that:
- angle A = 75°
- angle E = 30°
- angle D = angle X (since they are vertically opposite angles)
Using the exterior angle theorem, we know:
angle A=angle D+angle E
Substituting the known values:
75°=X+30°
Hint: Rearranging the equation will help you isolate X.
Step 6: Solve for X
Subtract 30° from both sides:
X=75°−30°
X=45°
Final Answer
The value of x is 45°.
---
Since AC = BC, triangle ABC is an isosceles triangle. This means that the base angles are equal. Given that angle C = 30°, we can find the other two angles.
Let the base angles be denoted as angle A and angle B. Since AC = BC, we have:
angle A=angle B
Using the triangle angle sum property:
angle A+angle B+angle C=180°
Substituting the known value:
angle A+angle A+30°=180°
This simplifies to:
2×angle A+30°=180°
Subtract 30° from both sides:
2×angle A=180°−30°
2×angle A=150°
Now divide both sides by 2:
angle A=75°
Since triangle ADE is similar to triangle ABC (as stated in the problem), the corresponding angles are equal. Therefore:
angle C=angle E
Thus:
angle E=30°
In triangle ADE, we know that:
- angle A = 75°
- angle E = 30°
- angle D = angle X (since they are vertically opposite angles)
angle A=angle D+angle E
Substituting the known values:
75°=X+30°
Subtract 30° from both sides:
X=75°−30°
X=45°
The value of x is 45°.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE45videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice99videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST24videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE6videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
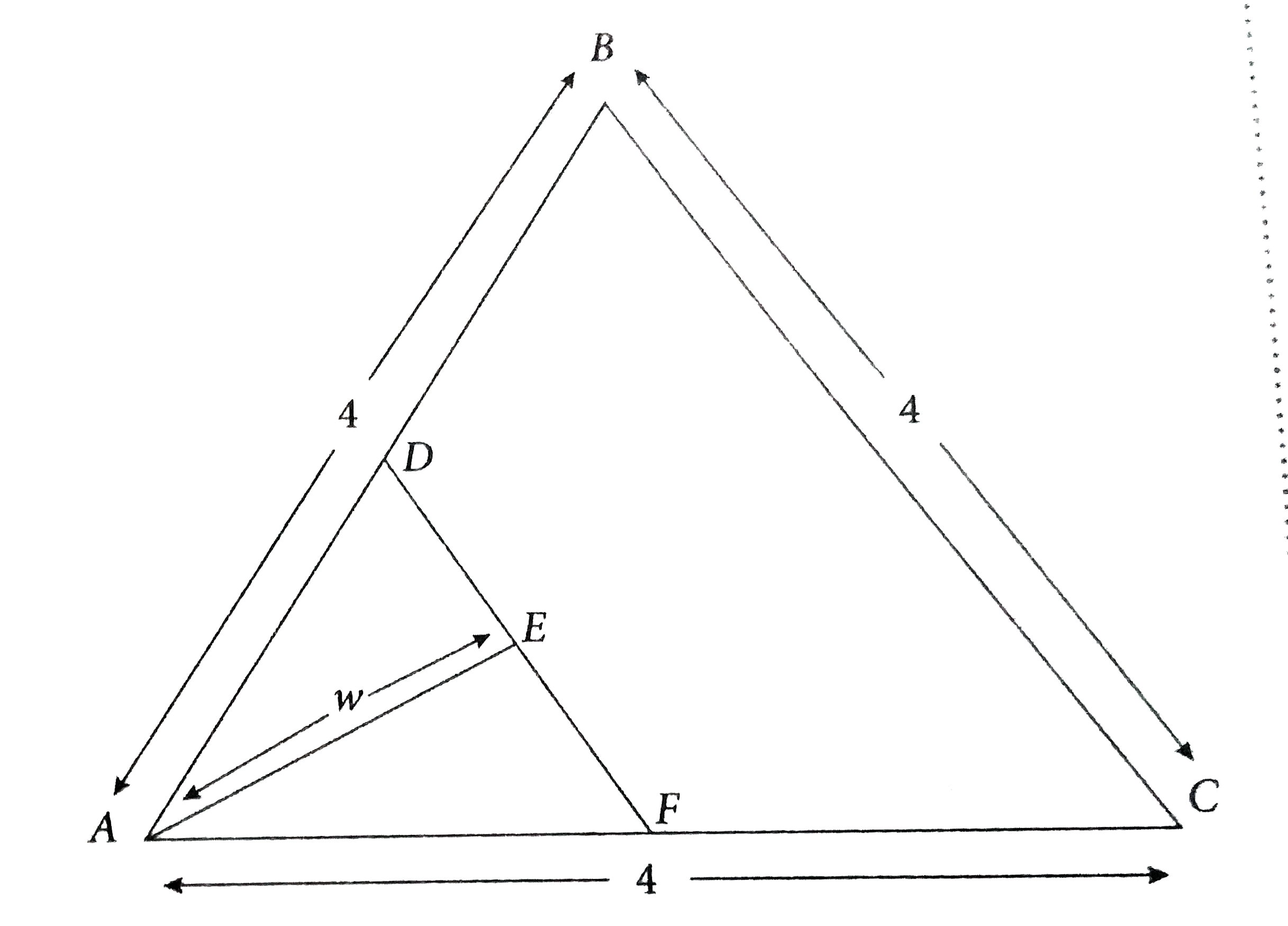
ΔABC is equilateral and ∠AEF is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?A1B√3C2D2√3
D is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn triangle ABC, the measure of ∠B is 90∘, BC = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 13 the length of the corresponding side of triangle ABC. What is the value of sin F ?
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=ECView Solution
¯¯¯¯¯¯ACand¯¯¯¯¯¯BD are diameters of circle E above. Which triangle congruence theorem can be used to prove that △AEB is congruent to △DEC?View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CDView Solution

