The bottom of a ske slope is 6,500 feet above sea level,the top of the slope is 11,000 feet above sea level, and the slope drops 5 feet vertically for every 11 feet traveled in the horizontal direction. From the top of the slope, Kayla skis down at an average speed of 30 miles per hour. Which of the following function gives the best estimate for the distance above sea level, d, Kayla is t seconds after she begins her ski run where 6,500<d<11,000?
d(t)=11,000−(15011)t
d(t)=11,000−2.2t
d(t)=11,000−20t
d(t)=4,500−1,200t
The correct Answer is:C
To solve the problem step by step, we will determine the function that estimates the distance above sea level, d, that Kayla is at t seconds after she begins skiing down the slope.
Step 1: Understand the height of the slope
The bottom of the ski slope is at 6,500 feet above sea level, and the top is at 11,000 feet above sea level. This means that Kayla starts skiing from a height of 11,000 feet.
Step 2: Determine the slope of the ski run
The slope drops 5 feet vertically for every 11 feet traveled horizontally. This gives us a slope ratio of:
slope=−511
The negative sign indicates that the height is decreasing as she skis down.
Step 3: Convert Kayla's speed to feet per second
Kayla skis down at an average speed of 30 miles per hour. To convert this speed to feet per second:
30 miles/hour=30×5280 feet/mile÷3600 seconds/hour
Calculating this gives:
30×5280=158400 feet/hour
1584003600=44 feet/second
Step 4: Calculate the descent per second
To find out how much Kayla descends vertically each second, we multiply her speed in feet per second by the slope:
Descent per second=44 feet/second×5 feet11 feet=20 feet/second
Step 5: Determine the total descent after t seconds
After t seconds, the total descent will be:
Total descent=20t feet
Step 6: Write the function for height above sea level
Starting from 11,000 feet, the height above sea level after t seconds will be:
d(t)=11000−20t
Conclusion
Thus, the function that gives the best estimate for the distance above sea level, d, Kayla is at t seconds after she begins her ski run is:
d(t)=11000−20t
The bottom of the ski slope is at 6,500 feet above sea level, and the top is at 11,000 feet above sea level. This means that Kayla starts skiing from a height of 11,000 feet.
The slope drops 5 feet vertically for every 11 feet traveled horizontally. This gives us a slope ratio of:
slope=−511
The negative sign indicates that the height is decreasing as she skis down.
Kayla skis down at an average speed of 30 miles per hour. To convert this speed to feet per second:
30 miles/hour=30×5280 feet/mile÷3600 seconds/hour
Calculating this gives:
30×5280=158400 feet/hour
1584003600=44 feet/second
To find out how much Kayla descends vertically each second, we multiply her speed in feet per second by the slope:
Descent per second=44 feet/second×5 feet11 feet=20 feet/second
After t seconds, the total descent will be:
Total descent=20t feet
Starting from 11,000 feet, the height above sea level after t seconds will be:
d(t)=11000−20t
Thus, the function that gives the best estimate for the distance above sea level, d, Kayla is at t seconds after she begins her ski run is:
d(t)=11000−20t
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One

Which of the following is most likely the slope of the line of best fit for the scatterplot above?A−10B−1C1D10 - Question 2 - Select One
A helicopter, initially hovering 40 feet above the ground, begins to gain altitude at a rate of 21 feet per second. Which of the following functions represents the helicopter’s altitude above the ground y, in feet, t seconds after the helicopter begins to gain altitude?
Ay = 40 + 21By = 40 + 21tCy = 40 − 21tDy = 40t + 21 - Question 3 - Select One
The front of a roller-coaster car is at the bottom of a hill and is 15 feet above the ground. If the front of the roller-coaster car rises at a constant rate of 8 feet per second, which of the following equations gives the height h, in feet, of the front of the roller-coaster car s seconds after it starts up the hill?
Ah = 8s + 15Bh=15s+3358Ch=8s+33515Dh = 15s + 8
A place is 27 m above sea level and another place is 14 m below sea level . What is the difference of level between two places ?
View SolutionWrite down the slopes of the following lines:
−6y−11x=0View SolutionThe Mount Everest is 29,029 feet above sea level. The deepest point in the Indian Ocean is the Java Trench at 25.344 feet. Find the vertical distance between the two.
View SolutionA ladder is placed with one edge on the wall 15 feet above the ground and the other end on the ground 8 feet away from the wall. Find the length of the ladder.
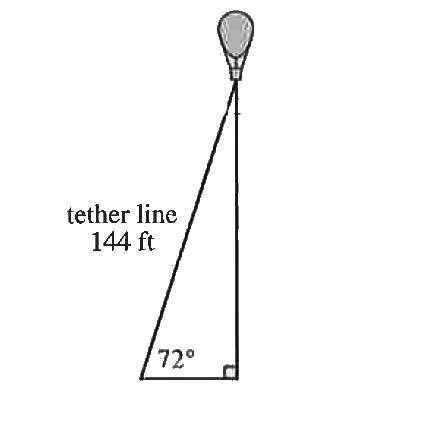
View SolutionThe bottom of the basket of a hot-air balloon is parallel to the level ground. One taut tether line 144 feet long is attached to the centre of the bottom of the basket and is anchored to the ground at an angle of 72∘, as shown in the figure below. Which of the following expressions gives the distance, in feet, from the center of the bottom of the basket to the ground?
 View Solution
View Solution

