A uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle α to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
ω=√(3gsinα2l)
ω=√(2l3gsinα)
ω=√(gsinαl)
ω=√(lgsinα)
The correct Answer is:A
To solve the problem, we will use the principles of conservation of energy and the moment of inertia of the rod. Here are the steps to find the angular velocity of the rod when it becomes horizontal:
1. Identify the Initial and Final States:
- The rod is initially inclined at an angle α to the horizontal.
- The length of the rod is 2L.
- The mass of the rod is m.
- When the rod becomes horizontal, we need to find its angular velocity ω.
2. Calculate the Initial Potential Energy:
- The center of mass of the rod is at a distance L from the hinge (the point in contact with the table).
- The height of the center of mass when the rod is inclined at angle α is given by:
h=Lsinα
- Therefore, the initial potential energy PEi is:
PEi=mgh=mg(Lsinα)
3. Calculate the Final Potential Energy:
- When the rod becomes horizontal, the height of the center of mass is 0, so the final potential energy PEf is:
PEf=0
4. Calculate the Initial and Final Kinetic Energy:
- Initially, the rod is at rest, so the initial kinetic energy KEi is:
KEi=0
- When the rod is horizontal, it has rotational kinetic energy given by:
KEf=12Iω2
- The moment of inertia I of the rod about the hinge point is:
I=13m(2L)2=43mL2
5. Apply Conservation of Energy:
- According to the conservation of mechanical energy:
PEi+KEi=PEf+KEf
- Substituting the values we calculated:
mg(Lsinα)+0=0+12(43mL2)ω2
6. Simplify the Equation:
- Cancel m from both sides (assuming m≠0):
gLsinα=23L2ω2
- Rearranging gives:
ω2=3gsinα2L
7. Find the Angular Velocity:
- Taking the square root of both sides:
ω=√3gsinα2L
Final Answer:
The angular velocity ω of the rod when it becomes horizontal is:
ω=√3gsinα2L
- The rod is initially inclined at an angle α to the horizontal.
- The length of the rod is 2L.
- The mass of the rod is m.
- When the rod becomes horizontal, we need to find its angular velocity ω.
- The center of mass of the rod is at a distance L from the hinge (the point in contact with the table).
- The height of the center of mass when the rod is inclined at angle α is given by:
h=Lsinα
- Therefore, the initial potential energy PEi is:
PEi=mgh=mg(Lsinα)
- When the rod becomes horizontal, the height of the center of mass is 0, so the final potential energy PEf is:
PEf=0
- Initially, the rod is at rest, so the initial kinetic energy KEi is:
KEi=0
- When the rod is horizontal, it has rotational kinetic energy given by:
KEf=12Iω2
- The moment of inertia I of the rod about the hinge point is:
I=13m(2L)2=43mL2
- According to the conservation of mechanical energy:
PEi+KEi=PEf+KEf
- Substituting the values we calculated:
mg(Lsinα)+0=0+12(43mL2)ω2
- Cancel m from both sides (assuming m≠0):
gLsinα=23L2ω2
- Rearranging gives:
ω2=3gsinα2L
- Taking the square root of both sides:
ω=√3gsinα2L
The angular velocity ω of the rod when it becomes horizontal is:
ω=√3gsinα2L
Similar Questions
A block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View SolutionA uniform rod of length l is kept vertically on a rough horizontal surface at x = 0 . It is rotated slightly and released . When the rod finally falls on the horizontal surface , the lower end will remain at

View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA rod of length l is siding such that one of its ends is always in contact with a vertical wall and its other end is always in contact with horizontal surface. Just after the rod is relased from rest, the magnitude of acceleration of end points of the rod is a and b respectively. The angular acceleration of road at this istant will be

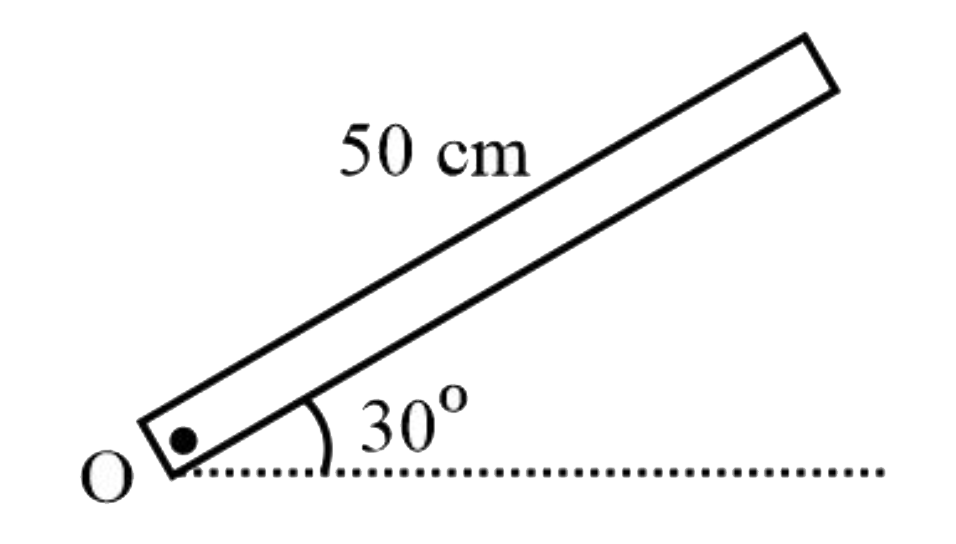
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
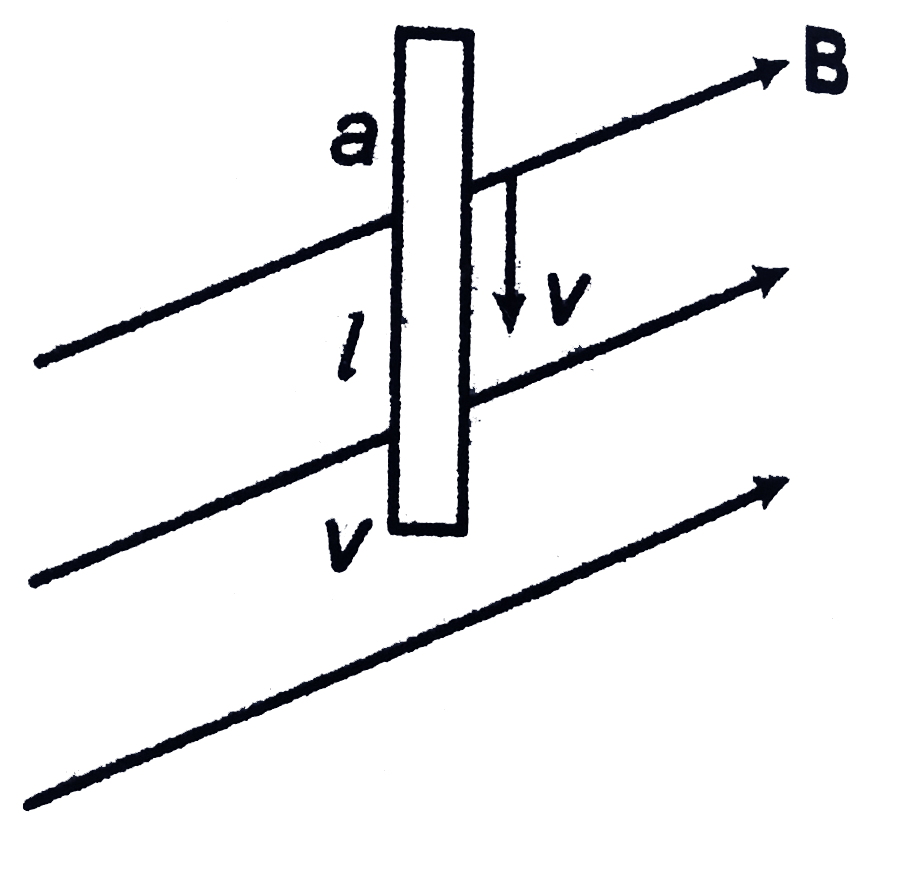
View SolutionA conducting rod of length l falls verticaly under gravity in a region of uniform magnetic field B. The field vectors are inclined at an angle θ with the horizontal as shown in figure. If the instantaneous velocity of the rod is v, the induced emf in the rod ab is
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View Solution
