A uniform rod of length l is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall, without slipping at contact point. When it becomes horizontal, its angular velocity will be

A

$ω = \sqrt{\frac{3 g sin α}{l}}$

B

$ω = \sqrt{\frac{2 l}{3 g sin α}}$

C

$ω = \sqrt{\frac{6 g sin α}{l}}$

D

$ω = \sqrt{\frac{l}{g sin α}}$

Text Solution

Verified by Experts

The correct Answer is:A

By principle of conservation of energy, potential energy of the rod is converted into rotational energy.
P.E. of rod= mg $. \frac{l}{2} sin α$
Rotational K.E. = $\frac{1}{2} I ω^{2} = \frac{1}{2} \frac{m l^{2}}{3} ω^{2}$
$m g \frac{l}{2} sin α = \frac{1}{2} . \frac{m l^{2}}{3} . ω^{2} \Rightarrow ω = \sqrt{\frac{3 g sin α}{l}}$

|

Updated on:21/07/2023

Class 12 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform rod of length $L$ is placed with one end in contact with the horizontal and is then inclined at an angle $α$ to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
A $ω = \sqrt{\frac{3 g sin α}{L}}$
B $ω = \sqrt{\frac{2 L}{3 g sin α}}$
C $ω = \sqrt{\frac{6 g sin α}{L}}$
D $ω = \sqrt{\frac{L}{g sin α}}$
Question 2 - Select One
A uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle $α$ to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
A $ω = \sqrt{(\frac{3 g sin α}{2 l})}$
B $ω = \sqrt{(\frac{2 l}{3 g sin α})}$
C $ω = \sqrt{(\frac{g sin α}{l})}$
D $ω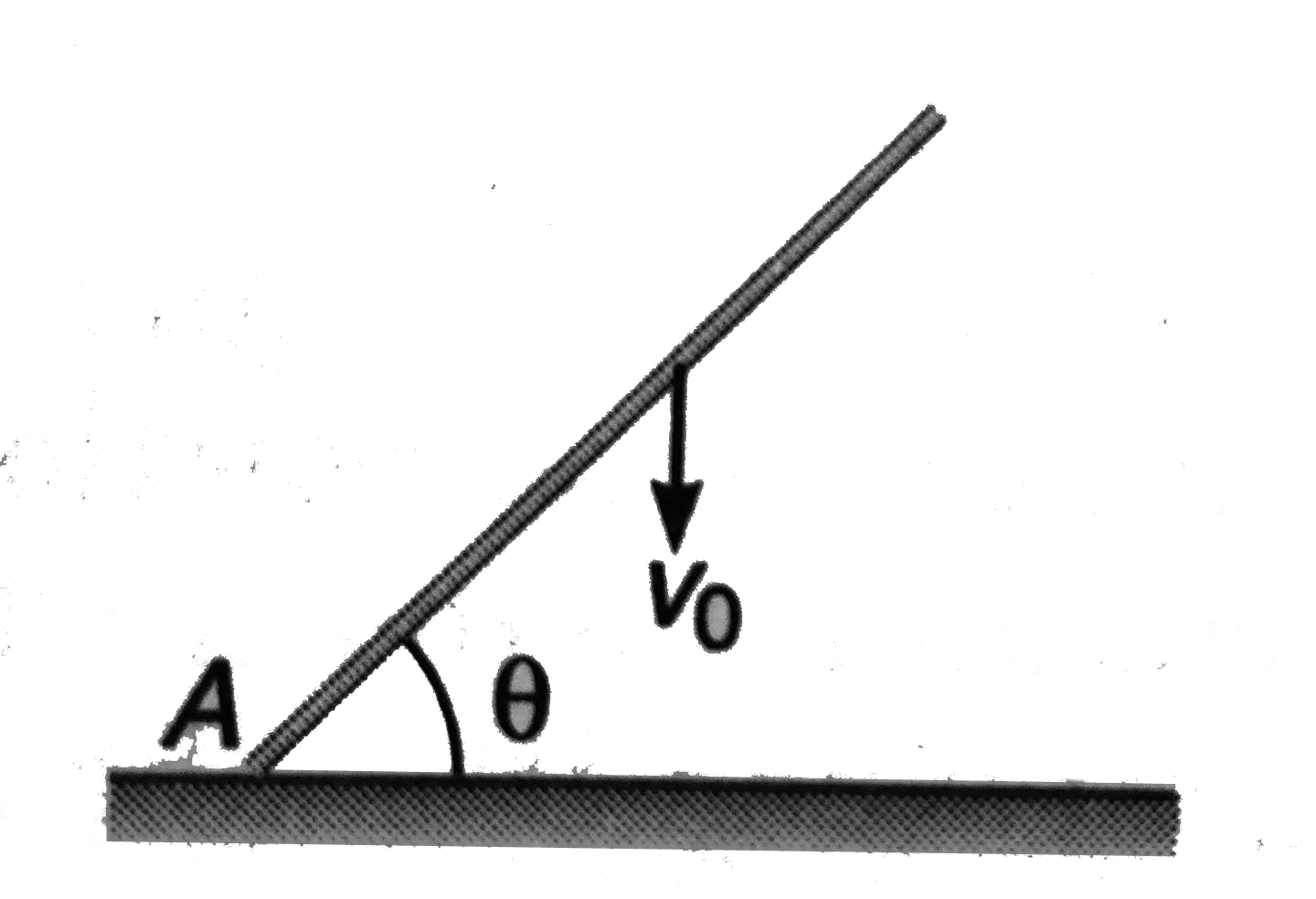 = \sqrt{(\frac{l}{g sin α})}$
Question 3 - Select One

A rod of length $l$ forming an angle $θ$ with the horizontal strikes a frictionless floor at A with its centre of mass velocity $v_{0}$ and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
A $\frac{3 v cos θ}{2 l}$
B $\frac{12 v cos θ}{l (1 + {cos}^{2}) θ}$
C $\frac{12 v cos θ}{l (1 + 3 {cos}^{2} θ)}$
D $\frac{v cos θ}{l (1 + {cos}^{2} θ)}$

MTG-WBJEE-MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTION-WB-JEE Previous years questions

Home
Ask Doubt
Profile