A pendulum is released from point A as shown in figure. At some instant net force one the bob is making an angle θ with the string. Then Match the following

Table-1Table-2(A)For θ=30∘(P)Particle may be moving along BA(B)For θ=120∘(Q)Particle may be moving along CB(C)For θ=90∘(R)Particle may be at A(D)For θ=0∘(S)Particle is at B(T)None
The correct Answer is:(A)QP,(B)T,(C)R,(D)S
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A pendulum is released from point A as shown in figure. At some instant net force on the bob is making and angle θ with the string. Then match the following:

Column-1 Column-2(A)Forθ=30∘(P) Particle may be moving between B & A(B)Forθ=120∘(Q) Particle may be moving between C & B particle is at A(C)Forθ=90∘(R) Particle is at A(D)Forθ=0∘(S) Particle is at B(T) None
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
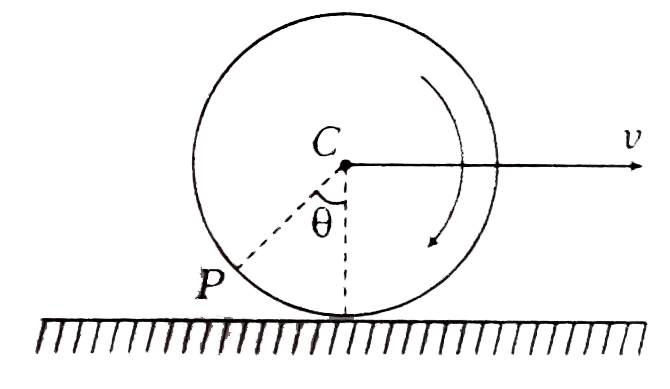
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View Solution
Knowledge Check
A particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
AVelocity of particle at Q is vsinθBVelocity of particle at Q is vcotθCTime of flight from P to Q is (v/g)cosecθDTime of flight from P to Q is (v/g)secθThe x−t graph of particle moving along a straight line is shown in figure

Two projectiles A and b are thrown will the same speed such that A makes anle θ with the horizontal and B makes angle θ with the vertical, thenABoth must have same time of flightBBoth must achieve same maximum heightCA must have more horizontal range the BDBoth may have same time of flightA particle is projected with a velocity of 30ms−1, at an angle of θ0=tan−1(34). After 1s, the particle is moving at an angle θ to the horizontal, where tanθ will be equal to (Take, g=10ms−2)
A1B2C12D13
A particle moves from position A to position B in a path as shown in If the poit vectors →r1 and →r2 making an angle θ between them are give, find the magnitude of displacement.
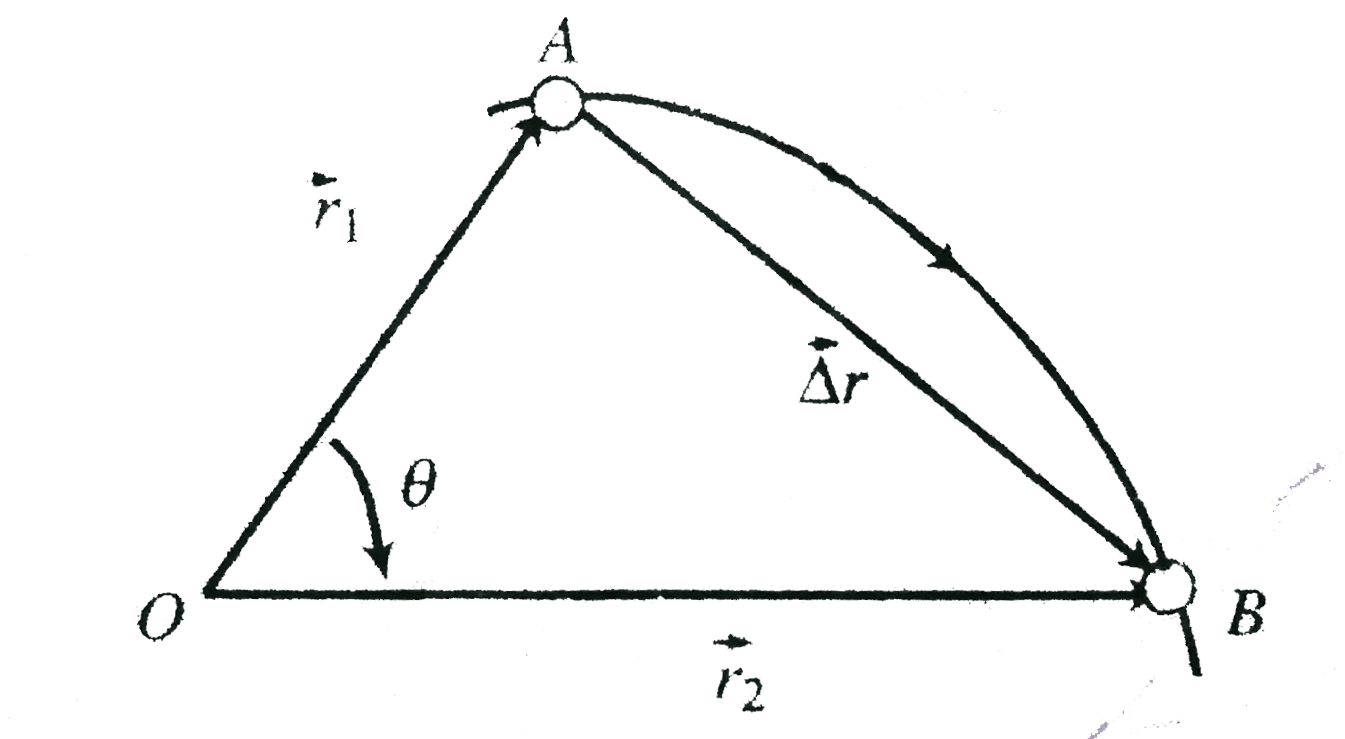 .
.
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected with a velocity of 30ms−1, at an angle of θ0=tan−1(34). After 1s, the particle is moving at an angle θ to the horizontal, where tanθ will be equal to (Take, g=10ms−2)
View SolutionIf θ is the angle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)None
View Solution
