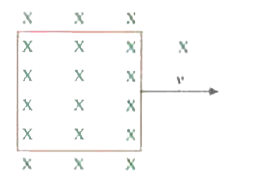
A square-shaped conducting wire loop of dimension a moving parallel to the x-axis approaches a square region of size b (a<b) where a uniform magnetic field B exists pointing into the plane of the paper (see figure). As the loop passes through this region, the plot correctly depicting its speed (v) as a function of x is




The correct Answer is:B
Step by step video, text & image solution for A square-shaped conducting wire loop of dimension a moving parallel to the x-axis approaches a square region of size b (a lt b) where a uniform magnetic field B exists pointing into the plane of the paper (see figure). As the loop passes through this region, the plot correctly depicting its speed (v) as a function of x is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
 View Solution
View SolutionA wire loop confined in a plane is rotated in its oen plane with some angular velocity. A uniform magnetic field exists in the region. Fid the emf induced in the loop.
02:43View SolutionA square loop of wire with resistance R is moved at constant speed v across a uniform magnet field confined to a square region whose sides are twice the lengths of those of the square loop
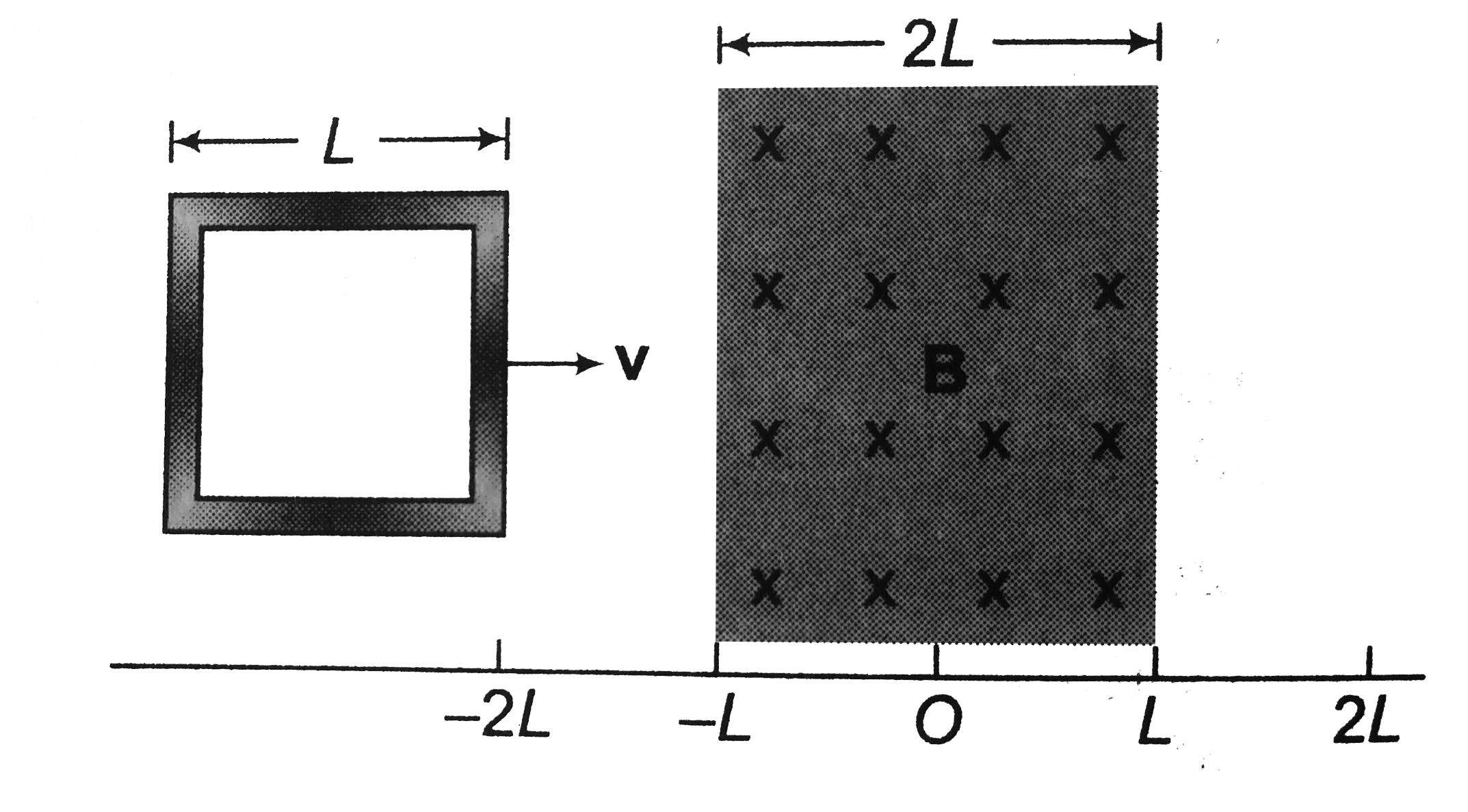
(a) Sketch a graph of the external forces F needed to move the loop at constant speed, as a function of to sketch a graph of the external force F need tho coordinate x, fromx=−2L to x=+2L. (The coordinate x is measured from the centre of the oignetic field region to the centre of the loop. It is negative when the centre of the loop is to the left, of the centre of the magnetic field region. Take positive force to be to the right). (b) Sketch a graph of the induced current in the loop as a function of x. Take counterclockwise currents to be positive.01:56View SolutionA square loop of wire carrying current I is lying in the plane of paper as shown in Fig. 1.141. The magnetic field is present in the region as shown. The loop will tend to rotate
 01:15View Solution
01:15View SolutionA square loop of side a and resistance R is moved in the region of uniform magnetic field B(loop remaining completely insidefield), with a velocity v through a distance x. The work done is:
06:02View SolutionA region of width L contains a uniform magnetic field B directed into the plane of the figure. A square conducing loop of side length l(<L) is kept with its side AB at the boundary of the field region (see Figure). The loop is pushed into the field region with a speed such that it just manages to exit the field region. Calculate the time needed for the entire loop to enter the field region after it is pushed. Mass and resistance of the loop is M and R respectively.
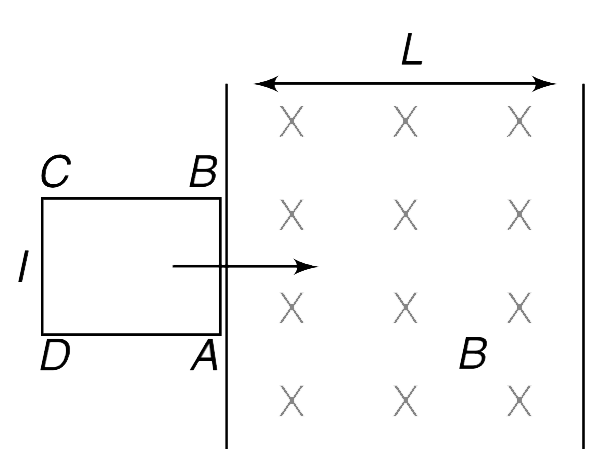 02:48View Solution
02:48View SolutionA square-shaped wire loop of mass m, resistance R and side 'a' moving with speed v0, parallel to the x-axis, enters a region of uniform magnetic field B, which is perpendicular to the plane of the loop. The speed of the loop changes with distance x (x<a) in the filed, as
06:48View SolutionA uniform magnetic field B=B_(0)that"i" in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
05:59View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R. Show the direction of the current when the loop is entering into the region II.
05:59View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R. Plot a graph between the induced emf and the time of rotation for two periods of rotation.
02:24View SolutionA conducting square loop of side L and resistance R moves in its to one of tis sides. A magnetic induction B , constant in time and space, pointing perpendicular to and into the plane of the loop exists every where. The current induced in the loop is
 08:13View Solution
08:13View SolutionA square loop of a conducting material of side l and resistance r is dragged through a uniform magnetic field B with uniform velocity v keeping the plane of the loop perpendicular to the direction of the field. What is the current flowing through the loop?
06:40View SolutionA circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
03:56View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
06:47View SolutionA square loop of wire with resistance R is moved at constant speed v across a uniform magnet field confined to a square region whose sides are twice the lengths of those of the square loop

(a) Sketch a graph of the external forces F needed to move the loop at constant speed, as a function of to sketch a graph of the external force F need tho coordinate x, fromx=−2L to x=+2L. (The coordinate x is measured from the centre of the oignetic field region to the centre of the loop. It is negative when the centre of the loop is to the left, of the centre of the magnetic field region. Take positive force to be to the right). (b) Sketch a graph of the induced current in the loop as a function of x. Take counterclockwise currents to be positive.02:52View Solution

