Gravitational field due to a solid sphere
remains constant throughout the sphere
increase inside the sphere and decreases outside the sphere
increases throughout with distance from the center
decreases throughout with distance from the centre
The correct Answer is:B
Graviational field due to a solid sphere
E(r)=GMR3r
⇒E(r)∝r, i.e., E(r) increases inside the sphere
E(r)=GMr2
⇒E(r)∝1r2,i.e. E(r) decreases outside the sphere.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.4
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Intensity Of Gravitaional Field Due To Solid Sphere
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
Knowledge Check
The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzeroAt some point the gravitational potential and also the gravitational field due to earth is zero. The point is
AOn earth's surfaceBBelow earth's surfaceCAt a height Re from earth's surface (Re= radius of the earth)DAt infinityIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
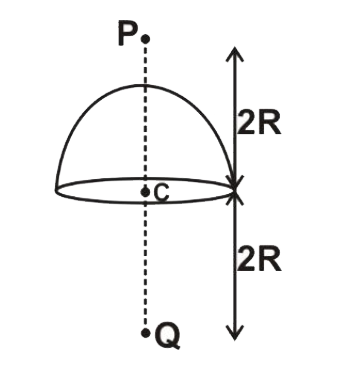 AGM2R2−IBGM2R2+ICGM4R−ID2I−GM2R2
AGM2R2−IBGM2R2+ICGM4R−ID2I−GM2R2
Match the entries given in column I with those given in column II.
Column IColumn II(A)Plot of gravitational field due to a uniform solid sphere with distance from its centre.(p)Continuos(B)Plot of gravitational field due to a thin spherical shell with distance from centre.(q)Discontinuos(C)Plot of gravitational potential due to a uniform solid sphere with distance from centre.(r)Straight line(D)Plot of gravitational potential due to a thin spherical shell with distance from centre.(s)Rectangular hyperbola(t)Parabola
View SolutionIntensity Of Gravitational Field Due To Hollow Sphere
View SolutionConsider two solid spheres of radii R1=1m,R2=2m and masses M1andM2 , respectively . The gravitational field due to sphere (1) and (2) are shown. The value of M1M2 is :
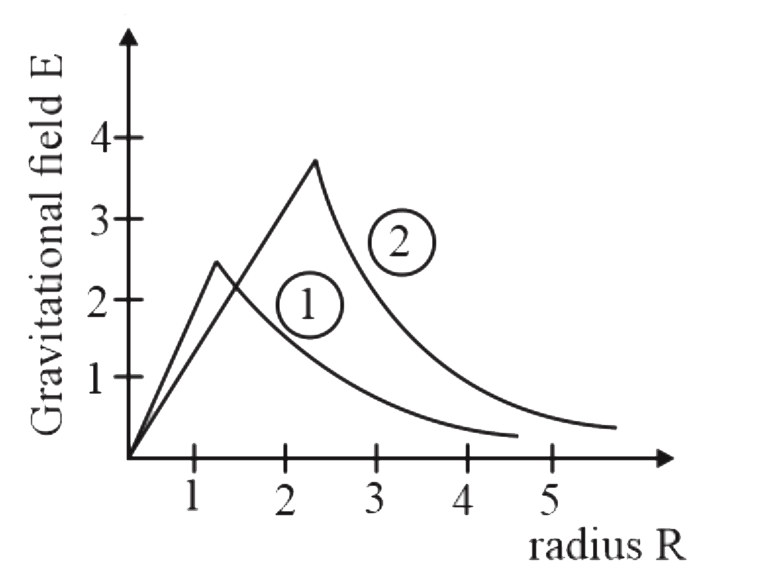
View SolutionGravitation field||Gravitation field due to Point charge||Gravitation field due to sphere and shell||Gravitation field due to a rod||Gravitation field due to a ring||Effect OF rotation OF earth||Effect OF shape OF earth
View SolutionElectric field due to spheres
View Solution
