Assertion : When two charged spheres are connected to each other by a thin conducting wire, charge flow bigger sphere to smaller sphere, if initial charges on them are same.
Reason : Electrostatic potential energy will be lost in redistribution of charges.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
229 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two identical conducting spheres, fixed in place, attract each other with an electrostatic force of 0.108 N when their center-to-center separation is 50.0 cm. The spheres are then connected by a thin conducting wire. When the wire is removed, the spheres repel each other with an electrostatic force of 0.144 N. Of the initial charges on the spheres, with a positive net charge, what was (a) the negative charge on one of them and (b) the positive charge on the other ?
View SolutionStatement-1 : If two concentric conducing sphere which are connected by a conducting wire. No charge can exist on inner sphere.
Statement-2: When charge on outer sphere will exist then potential of inner shell and outer shell will be same.
View Solution
Knowledge Check
When these two spheres are made to touch with each other, then final charge on bigger sphere will be
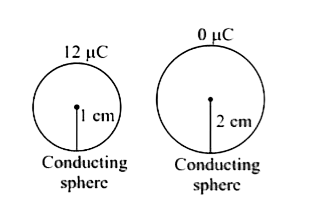 A0μCB12μCC4μCD8μC
A0μCB12μCC4μCD8μCWhen two spheres carrying same charge but a different radii are connected by a conducting wire, the charge flows from smaller sphere to large sphere.
Smaller sphere is at high potential when equal charges are imparted to both the spheres.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A.Statement-1 : If two concentric conducing sphere which are connected by a conducting wire. No charge can exist on inner sphere.
Statement-2: When charge on outer sphere will exist then potential of inner shell and outer shell will be same.AStatement-1 is True, Statement-2 is True, Statement-2 is a cor.BStatement-1 is True, Statement-2 is True, Statement-2 is not aCStatement-1 is False, Statement-2 is TrueDStatement-1 is True, Statement-2 is False.
Two metallic spheres of radii a and b are placed faraway from each other and are connected for a thin conducting wire. A charge Q is given to one of the spheres . Calculate the charge on each sphere at electrostatic equilibrium.
View SolutionTwo metallic spheres of radii a and b are placed faraway from each other and are connected for a thin conducting wire. A charge Q is given to one of the spheres . Calculate the charge on each sphere at electrostatic equilibrium.
View SolutionA solid conducting sphere holds more charge than a hollow sphere of the same radius when they are at same potential.
View SolutionAssertion : Spherical shell a in the shown figure has a charge −q and shell B has charge +q. When these two are connected by a thin conducting wire, then whole of the electrostatic potential energy stored between the shell is lost.
Reason : Whole of the inner charge will transfer to outer shell B.
View SolutionAssertion : Spherical shell a in the shown figure has a charge −q and shell B has charge +q. When these two are connected by a thin conducting wire, then whole of the electrostatic potential energy stored between the shell is lost.
Reason : Whole of the inner charge will transfer to outer shell B.
View Solution
