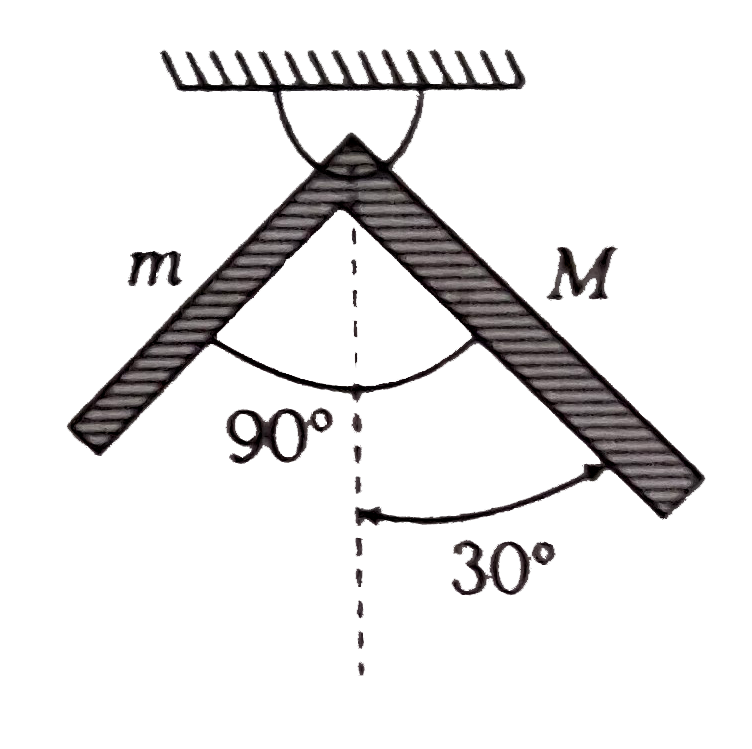
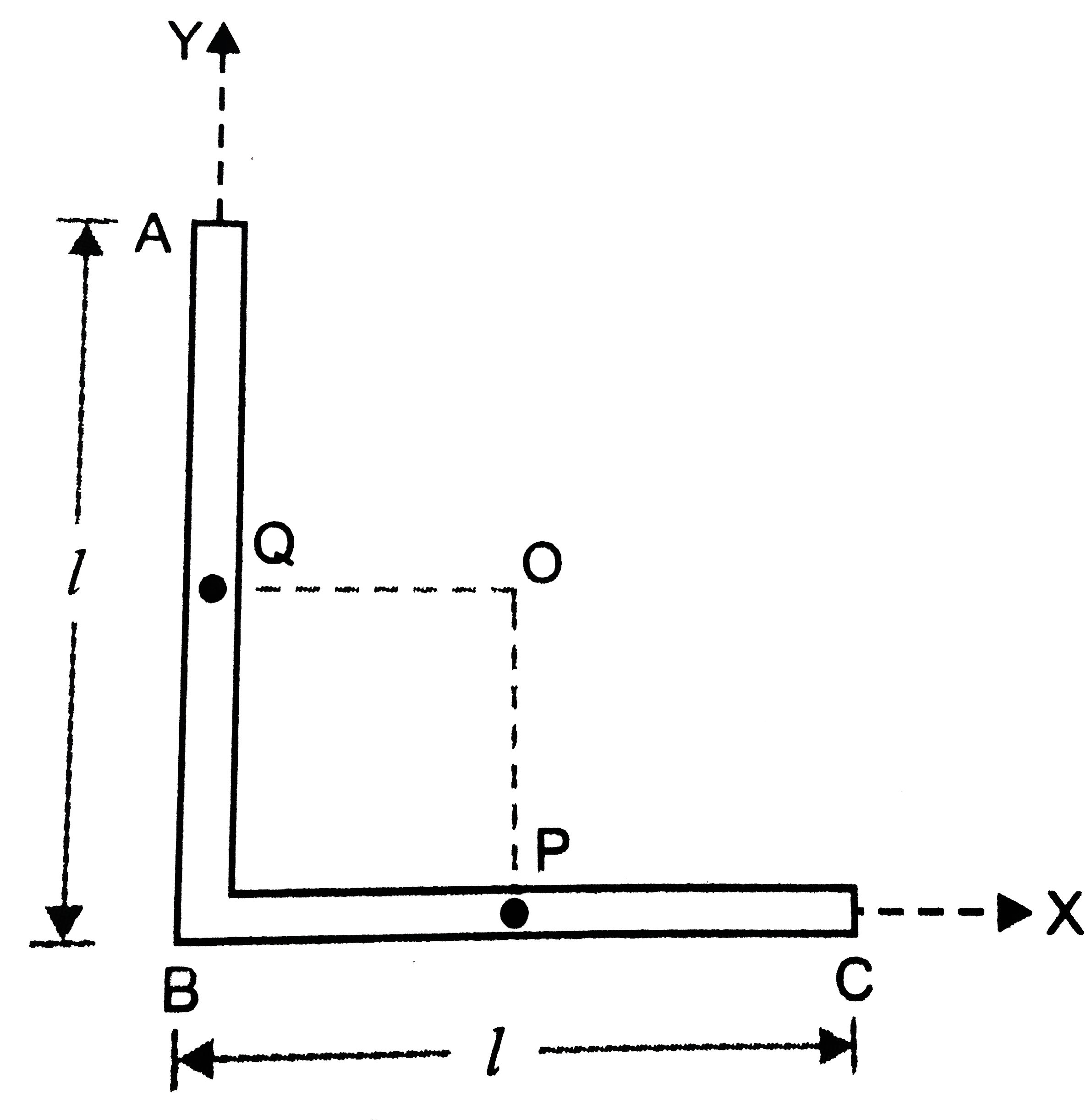
Two uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shown in figure. If in equilibrium the body is in the shown configuration, ratio M/m will be
2
3
√2
√3
The correct Answer is:D
Net torque about O should be zero
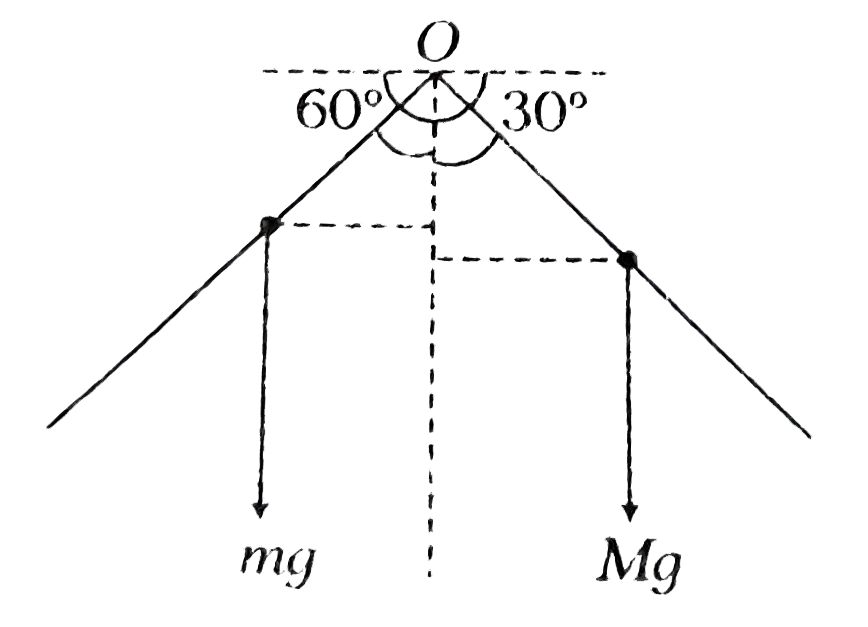
∴Mg12sin30∘=mg12sin60∘
Mm=sin60∘sin30∘=√3.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
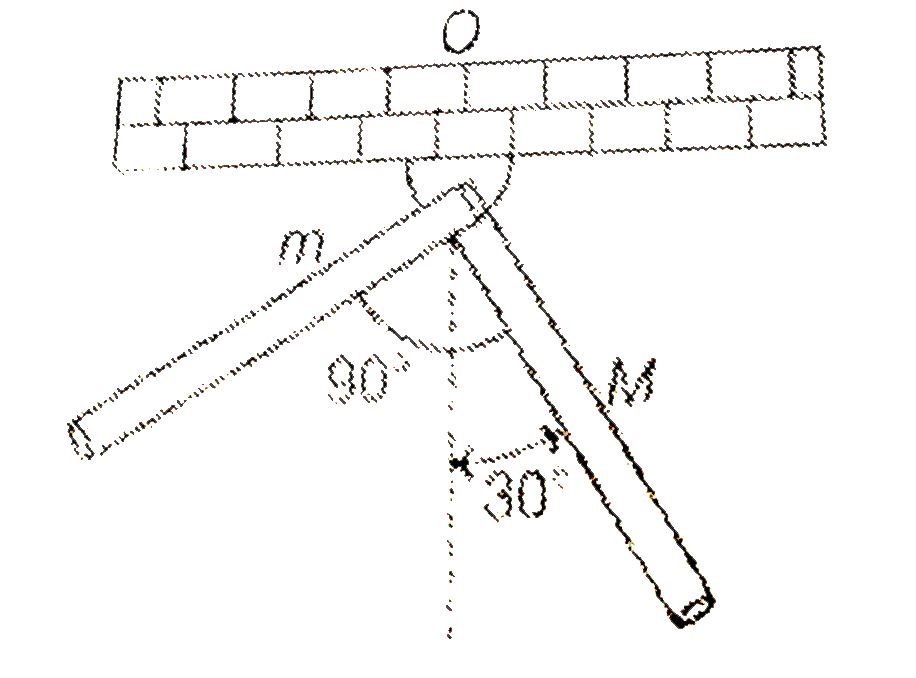
Two uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shwon. If in equilibrium, the body is in the shown configuration, ratio M//m will be
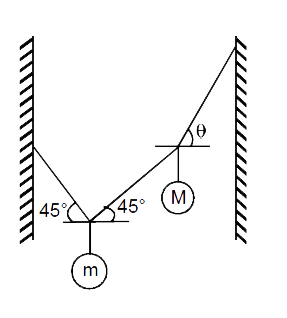
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View Solution
Knowledge Check
Two uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shwon. If in equilibrium, the body is in the shown configuration, ratio M//m will be
 A√2B2C√3D3
A√2B2C√3D3Two uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted about O as shown. If in equilibrium the body is in the shown configuration, ratio Mm will be
 A2B3C√2D√3
A2B3C√2D√3Two uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shwon. If in equilibrium, the body is in the shown configuration, ratio M//m will be
 A2B3C√2D√3
A2B3C√2D√3
Two identical uniform rods of length l are joined to from L shaped frame, as shown is Fig. Locate the centre of mass of the frame.
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then

View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
View Solution
