A portion of a ring of radius R has been removed as shown in figure. Mass of the remaining portion is m. Centre of the ring is at origin O. Let IAandIO be the moment of inertia passing through points A and O are perpendicular to the plane of the ring. Then,

IO=mR2
IO=IA
IO>IA
IA>IO
The correct Answer is:D
Whole mass has equal distance from the centre O. Hence, I0mR2. Further centre of mass of the remaining portion will be to the left of point O. More the distance of axis from centre of mass,more is the moment of inertia. Hence, IA>I0
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View Solution
Knowledge Check
A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… .
A0.0625kgm2B0.625kgm2C6.25kgm2D62.5kgm2Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A52MR2B32MR2C12MR2DMR2Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
AMR2B12MR2C32MR2D72MR2
A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
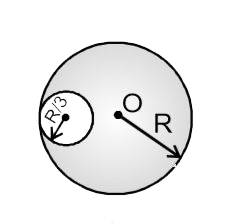
View SolutionFrom a disc of radius r1, a concentric disc of radius r2 is removed . The mass of the remaining portion is m. Find the M.I. of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View SolutionFrom a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is IA. If IC is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C, then

View SolutionA square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :

View Solution
