A neutron makes a head-on elastic collision with a stationary deuteron. The fraction energy loss of the neutron in the collision is

A

$16 / 81$

B

$8 / 9$

C

$8 / 27$

D

$2 / 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let mass of neutron = m, then mass of deutron = 2m

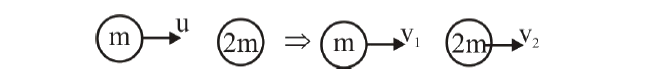
By Momentum conservation
mu = $m v_{1} + 2 m V_{2} \Rightarrow u = V_{1} + 2 v_{2} \dots . (2)$
( Elasic collision ) $u = v_{2} - V_{1} \dots . . (2)$
by equation (1) & (2) $V_{1} = - \frac{u}{3}$
Fractional loss of KE of neutron = $\frac{K E_{i} - K E_{f}}{K E_{i}}$
$= \frac{\frac{1}{2} m u^{2} - \frac{1}{2} m {(\frac{u}{3})}^{2}}{\frac{1}{2} m u^{2}} = 1 - \frac{1}{9} = \frac{8}{9}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A neutron makes is a head - on elastic collision with a stationary deuteron The fraction energy loss of the neutron in the collision is
A $16 / 81$
B $8 / 9$
C $8 / 27$
D $2 / 3$
Question 2 - Select One
A particle of mass $m$ moving with kinetic energy $K$ , makes a head - on elastic collision with a stationary particle of mass $η m$ . The maximum potential energy stored in the system during the collision is
A $\frac{η}{η + 1} K$
B $\frac{η + 1}{η} K$
C $(η - 1) K$
D $(η - 1) K$
Question 3 - Select One
An hydrogen atom moves with a velocity u and makes a head on inelastic collision with another stationary H-atom. Both atoms are in ground state before collision. The minimum value of u if one of them is to be given a minimum excitation energy is
A $2.64 \times 10^{4} m s^{- 1}$
B $6.24 \times 10^{4} m s^{- 1}$
C $2.02 \times 10^{6} m s^{- 1}$
D $6.24 \times 10^{8} m s^{- 1}$

NEET MAJOR TEST (COACHING)-NEET MAJOR TEST 10-PHYSICS

Home
Ask Doubt
Profile