Ticket prices for a school play are $7.50 for students and $10.00 for adults . For a given performance , 200 tickets were sold , and the performance took in $1,775. Solving which of the following systems of equations yields the number of student tickets , x , and the number of adult ticket , y, that were bought for that performance ?
x+y=200
7.5x+10y=1,775
x+y=1,775
7.5x+10y=200
x+y=200
7.5x+10y=1,7752
x+y=1,775
7.5x+10y=(1,775)(2)
The correct Answer is:A
To solve the problem, we need to set up a system of equations based on the information given about ticket sales for a school play.
Step 1: Define Variables
Let:
- x = number of student tickets sold
- y = number of adult tickets sold
Step 2: Set Up the First Equation
According to the problem, the total number of tickets sold is 200. Therefore, we can write the first equation as:
x+y=200
Step 3: Set Up the Second Equation
The total revenue from ticket sales is $1,775. The revenue from student tickets is 7.50x and from adult tickets is 10.00y. Thus, we can write the second equation as:
7.5x+10y=1775
Step 4: Write the System of Equations
Now we have the following system of equations:
1. x+y=200
2. 7.5x+10y=1775
Step 5: Solve the System of Equations
We can solve this system using substitution or elimination. Here, we will use substitution.
From the first equation, we can express y in terms of x:
y=200−x
Now, substitute y in the second equation:
7.5x+10(200−x)=1775
Step 6: Simplify and Solve for x
Distributing the 10:
7.5x+2000−10x=1775
Combine like terms:
−2.5x+2000=1775
Subtract 2000 from both sides:
−2.5x=1775−2000
−2.5x=−225
Now, divide by -2.5:
x=−225−2.5=90
Step 7: Solve for y
Now substitute x back into the equation for y:
y=200−x=200−90=110
Final Answer
Thus, the number of student tickets sold is x=90 and the number of adult tickets sold is y=110.
Let:
- x = number of student tickets sold
- y = number of adult tickets sold
According to the problem, the total number of tickets sold is 200. Therefore, we can write the first equation as:
x+y=200
The total revenue from ticket sales is $1,775. The revenue from student tickets is 7.50x and from adult tickets is 10.00y. Thus, we can write the second equation as:
7.5x+10y=1775
Now we have the following system of equations:
1. x+y=200
2. 7.5x+10y=1775
We can solve this system using substitution or elimination. Here, we will use substitution.
y=200−x
7.5x+10(200−x)=1775
Distributing the 10:
7.5x+2000−10x=1775
−2.5x+2000=1775
−2.5x=1775−2000
−2.5x=−225
x=−225−2.5=90
Now substitute x back into the equation for y:
y=200−x=200−90=110
Thus, the number of student tickets sold is x=90 and the number of adult tickets sold is y=110.
Topper's Solved these Questions
Similar Questions
Tickets for a school talent show cost $2 for students and $3 for adults. If Chris spends at least $11 but no more than $14 on x student tickets and 1 adult ticket, what is one possible value of x ?
View SolutionTickets to play cost $10 for children and $25 for adultes. If 90 tickets were sold, were more adult tickets sold than chidren's tickets?
(1) The average revenue per ticket was $18.
(2) The revenue from ticket sales exceeded $1,750
View Solution
Knowledge Check
Tickets for a concert cost $4.50 for children and $12.00 for adults. 4460 concert tickets were sold for a total cost of $29,220. Solving which of the following systems of equations yeilds the number of children, c, and numbr of adults, a, that purchased concert tickets?
Ac+a=4460
4.50+12a=58.440Bc+a=4460
4.50c+12a=29,220Cc+a=4460
4.50c+12a=14,610Dc+a=29,220
4.50c+12a=4460Two types of tickets were sold for a concert held at an amphitheater. Tickets to sit on a bench during the concert cost $75 each, and tickets to sit on the lawn during the concert cost $40 each. Organizers of the concert announced that 350 tickets had been sold and that $19,250 had been raised through ticket sales alone. Which of the following systems of equations could be used to find the number of tickets for bench seats, B, and the number of tickets for lawn seats, L, that were sold for the concert?
A(75B)(40L)=1,950
B+L=350B40B + 75L = 19,250
B+L=350C75B + 40L =350
B+L=19,250D75B+40L=19,250
B+L=350Bailey's Boutique Clothing is having a 20% off sale during which shirts cost $30.00 and pants cost $60.00. On the day of the sale, Bailey's sells a total of 60 shirts and pants and earned a total of $2,250. On a regular day, Bailey's sells 23 the number of shirts and pants sold during the sale and earns a total of $1,875. Solving which of the following system of equations yields the number of shirts,s, and the number of pants,p, sold during a regular day?
As+p=40
37.5s+75p=1,875Bs+p=40
30s+60p=2,250Cs+p=60
30s+60p=2,250Ds+p=2,250
30s+60p=60
The number of students absent in a class were recorded every day for 120 days and the information is given in the following frequency table: No. of students absent (x) : 0 1 2 3 4 5 6 7 No. of days (f) : 1 4 10 50 34 15 4 2 Find the mean number of students absent per day.
View SolutionTickets to the annual Follies Show at Littleton High School are $4 for adults and $2.50 for students. There is a cost of $750 to produce the show. If the x-axis represents the number of adult tickets sold and the y-axis represents the number of student tickets sold, which graph represents all the possible combinations of ticket sales that allow the junior class to at least cover the cost of the show ?
View SolutionEach student in the choir must earn $2500 to attend a performance in Ireland this summer. To earn the funds they are selling candy bars and t-shirts. For each candy bar sold, the singer earns $1 credit, and for each t-shirt the singer earn $5.75. Which equation represents the number of candy bars (X) and t-shirts (y) that must be sold by each singer to ensure that he/she can attend the performance ?
View SolutionCrowdfunding is a popular way to raise money using the Internet The process sounds simple an artist, entrepreneur, or other innovator takes his or her ideas straight to the public via a crowdfunding webs. The innovator creates a video about the project and offers, in exchange for donations, a series of perks," from acknowledgment on a social media site to a small piece of art. Many crowdfunding programs are all-or-nothing, In other words, the innovator must garner 100 percent funding for the project or the money is refunded to the donors. At it's best, the system can give creators direct access to millions of potential backers. The home page of one leading crowdfunding site features a project to manufacture pinhole cameras on a 3-D printer. Ea The idea is obviously very attractive. An obscure method of photography may be made available to many with little expense. Within weeks, the project was 621 percent funded. in contrast, on the same page, a small Brooklyn performance venue is attempting to raise money for its current season. The venue features works of performance art showcased in a storefront window. Those who have seen the space consider it vital. low ever, that group may not be large enough, with iu•t fourteen days to go in the fund raising period, the campaign is only 46 percent funded.
Artists such as these Brooklyn performers find that crowdfunding exacerbates problems that already exist. El Work, that is easily understood and appreciated, is supported, while more complex work goes unnoticed. Time that could be used creating art is spent devising clever perks to draw the attention of potential contributors. 28 In addition, audiences may contain many 'free riders," they did not make contributions.
ironically, the success of crowdfunding may weaken overall funding for the arts if people begin to feel that paying for the art 30 loved by them is someone else's responsibility. til One innovative playwright has woven the deficiencies of the system into her crowdfunding model. 121 Though the price for her tickets was higher than that of tickets for comparable shows, it was still affordable to most theatergoers—and reflected the real cost of the performance. [3] She presented the total cost for producing her play on a crowdfunding site. [4] Then she divided the total cost by the number of people she expected to attend the performance. [5) The result of the calculation was the minimum donor price, and only donors who paid at least the minimum ticket price were allowed to attend the performance. [6) By subverting the presumption that money used for her project is an altruistic donation, the playwright showed that W our work has monetary value to those who enjoy It.
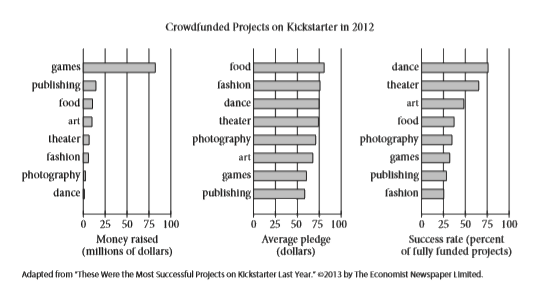
Which choice offers an accurate interpretation of the data in the graph?
View SolutionCrowdfunding is a popular way to raise money using the Internet The process sounds simple an artist, entrepreneur, or other innovator takes his or her ideas straight to the public via a crowdfunding webs. The innovator creates a video about the project and offers, in exchange for donations, a series of perks," from acknowledgment on a social media site to a small piece of art. Many crowdfunding programs are all-or-nothing, In other words, the innovator must garner 100 percent funding for the project or the money is refunded to the donors. At it's best, the system can give creators direct access to millions of potential backers. The home page of one leading crowdfunding site features a project to manufacture pinhole cameras on a 3-D printer. Ea The idea is obviously very attractive. An obscure method of photography may be made available to many with little expense. Within weeks, the project was 621 percent funded. in contrast, on the same page, a small Brooklyn performance venue is attempting to raise money for its current season. The venue features works of performance art showcased in a storefront window. Those who have seen the space consider it vital. low ever, that group may not be large enough, with iu•t fourteen days to go in the fund raising period, the campaign is only 46 percent funded.
Artists such as these Brooklyn performers find that crowdfunding exacerbates problems that already exist. El Work, that is easily understood and appreciated, is supported, while more complex work goes unnoticed. Time that could be used creating art is spent devising clever perks to draw the attention of potential contributors. 28 In addition, audiences may contain many 'free riders," they did not make contributions.
ironically, the success of crowdfunding may weaken overall funding for the arts if people begin to feel that paying for the art 30 loved by them is someone else's responsibility. til One innovative playwright has woven the deficiencies of the system into her crowdfunding model. 121 Though the price for her tickets was higher than that of tickets for comparable shows, it was still affordable to most theatergoers—and reflected the real cost of the performance. [3] She presented the total cost for producing her play on a crowdfunding site. [4] Then she divided the total cost by the number of people she expected to attend the performance. [5) The result of the calculation was the minimum donor price, and only donors who paid at least the minimum ticket price were allowed to attend the performance. [6) By subverting the presumption that money used for her project is an altruistic donation, the playwright showed that W our work has monetary value to those who enjoy It.
Which choice most effectively combines the underlined sentences?
View Solution
