A scale drawing of a new building has 12 inch representing 40 feet . If a conference room has a floor length of 60 feet , what is the floor length , in inches , on the scale drawing ?
34
78
1
112
The correct Answer is:A
To find the floor length of the conference room in inches on the scale drawing, we can follow these steps:
Step 1: Understand the scale
The scale given is 12 inch represents 40 feet.
Step 2: Determine how many feet are represented by 1 inch
Since 12 inch represents 40 feet, we can find out how many feet are represented by 1 inch by doubling this value:
1 inch=2×40 feet=80 feet
Step 3: Set up the proportion for the conference room
The conference room has a floor length of 60 feet. We need to find out how many inches this length represents on the scale drawing. Since we know that 1 inch represents 80 feet, we can set up the following proportion:
Length in inches=Actual length in feetFeet per inch=60 feet80 feet/inch
Step 4: Calculate the length in inches
Now we can perform the calculation:
Length in inches=6080=34 inch
Final Answer
The floor length of the conference room on the scale drawing is 34 inch.
---
The scale given is 12 inch represents 40 feet.
Since 12 inch represents 40 feet, we can find out how many feet are represented by 1 inch by doubling this value:
1 inch=2×40 feet=80 feet
The conference room has a floor length of 60 feet. We need to find out how many inches this length represents on the scale drawing. Since we know that 1 inch represents 80 feet, we can set up the following proportion:
Length in inches=Actual length in feetFeet per inch=60 feet80 feet/inch
Now we can perform the calculation:
Length in inches=6080=34 inch
The floor length of the conference room on the scale drawing is 34 inch.
Topper's Solved these Questions
Similar Questions
Frank the Fencemaker needs to fence in a rectangular yard. He fence in three of four sides of the yard. The unfenced side of the yard is 40 feet long. The yard has an area of 280 square feet. What is the length , in feet, of the fence that Frank installs?
View SolutionA new homeowner drew a floor plan of her new house, in which 1 inch on the floor plan in equivalent to 18 inches on the actual floor. If the actual longest side of the floor in one of the bedrooms is 153 inches, what is the length of the longest side of the same bedroom in the floor plan?
View Solution
Knowledge Check
- Question 1 - Select One
A sector of a circle has an arc length of 2.4 feet and an area of 14.3 square feet. How many degrees are in the central angle?
A63.4∘B20.2∘C14.3∘D11.5∘ - Question 2 - Select One
A circle has a radius that is the same length as the sides of a square , if the square has a perimeter of 64 square inches , what is the area , in square inches , of the circle ?
A16B16πC32πD256π - Question 3 - Select One
A table screen has a 12-inch diagonal. If the length of the screen is √3 times longer than the width, what is the area, in square inches, of the screen ?
A12B12√3C36D36√3
If a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
View SolutionThe top surface of a rectangular table has an area of 100 square feet and a width of 5 feet. What is the length, in feet, of the surface?
View SolutionIf a rectangular swimming pool has a volume of 16,500 cubic feet, a uniform depth of 10 feet, and a length of 75 feet, what is the width of the pool, in feet?
View SolutionWhen an elastic object , such as a coil spring or rubber band, is subjected to a force f, an increase in length , called a strain , occurs . Hooke's law states that force f is directly porportional to strain s. Suppose that a coil spring has a natural length of 4 feet and that a force of 60 pounds stretches the length to 6 feet. What magnitude of force , in pounds , would stretch the spring to a length of 7 feet ?
View SolutionFor △ABC shown below, base ¯¯¯¯¯¯AC has a length of 16 inches and altitude ¯¯¯¯¯¯BD has a length of 8 inches. The area of a certain square is equal to the area of △ABC. What is the length, in inches, of a side of the square?
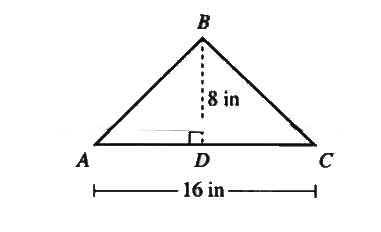 View Solution
View Solution

