As dry air moves upward , it expands and cools. If the temperature on the ground is 20∘ C and the temperature at a height of 1 km is 10∘ C, which of the following linear models best describes the temperature t in degrees C at a height of h km above the ground ?
t=−110h+20
t=110h+20
t=-10h+20
t=10h+20
The correct Answer is:C
To solve the problem step by step, we need to find a linear model that describes the relationship between temperature T (in degrees Celsius) and height h (in kilometers) based on the given data.
Step 1: Understand the given information
We know:
- The temperature at ground level (when h=0) is T=20∘C.
- The temperature at a height of 1 km (when h=1) is T=10∘C.
Step 2: Set up the linear equation
We assume a linear relationship between temperature T and height h:
T=a⋅h+b
where a and b are constants we need to determine.
Step 3: Use the first data point
From the first data point, when h=0:
T=20⟹20=a⋅0+b⟹b=20
Step 4: Substitute b into the equation
Now substituting b back into the linear equation:
T=a⋅h+20
Step 5: Use the second data point
From the second data point, when h=1:
T=10⟹10=a⋅1+20
This simplifies to:
10=a+20
Subtracting 20 from both sides gives:
a=10−20=−10
Step 6: Write the final equation
Now substituting the value of a back into the equation:
T=−10⋅h+20
Step 7: Identify the correct model
The linear model that describes the temperature T at height h is:
T=−10h+20
This matches with option 3 from the provided choices.
Final Answer
Thus, the correct linear model is:
T=−10h+20
---
We know:
- The temperature at ground level (when h=0) is T=20∘C.
- The temperature at a height of 1 km (when h=1) is T=10∘C.
We assume a linear relationship between temperature T and height h:
T=a⋅h+b
where a and b are constants we need to determine.
From the first data point, when h=0:
T=20⟹20=a⋅0+b⟹b=20
Now substituting b back into the linear equation:
T=a⋅h+20
From the second data point, when h=1:
T=10⟹10=a⋅1+20
This simplifies to:
10=a+20
Subtracting 20 from both sides gives:
a=10−20=−10
Now substituting the value of a back into the equation:
T=−10⋅h+20
The linear model that describes the temperature T at height h is:
T=−10h+20
This matches with option 3 from the provided choices.
Thus, the correct linear model is:
T=−10h+20
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
As the temperature is raised from 20∘C to 40∘C, the average kinetic energy of neon atoms changes by a factor of which of the following?
A12B√313293C313293D2 - Question 2 - Select One
a=1,052+1.08t
The speed of a sound wave in air depends on the air temperature. The formula above shows the relationship between a, the speed of a sound wave, in feet per second, and t, the air temperature, in degrees Fahrenheit (.∘F).
Which of the following expresses the air temperature in terms of the speed of a sound wave?At=a−1,0521.08Bt=a+1,0521.08Ct=1,052−a1.08Dt=1.08a+1,052 - Question 3 - Select One
A block of ice, initially at −20∘C, is heated a steady rate until the temperature of the sample reaches 120∘C. Which of the following graphs best illustrates the temperature of the sample as a function of time?
A B
B C
C D
D
A body cools in 10 minutes from 60∘C to 40∘C. What is the temperature of the body after next 20 minutes? The temperatuer fo surroundings is 10∘C
View SolutionFind the temperature at which the velocity of sound in air will be 112 times of the velocity at 27∘C.
View SolutionA sphere, a cube and a thin circular plate, all made of the same mass and finish are heated to a temperature of 200∘C. Which of these objects will cool slowest, when left in air at room temperature?
View Solution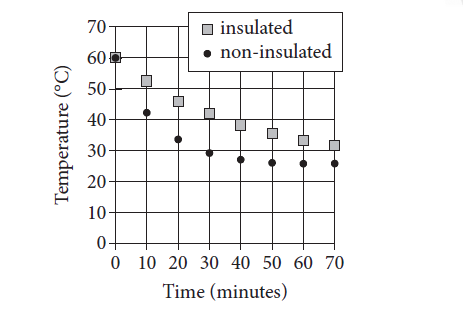
Two samples of water of equal mass are heated to 60 degrees Celsius (°C). One sample is poured into an insulated container, and the other sample is poured into a non-insulated container. The samples are then left for 70 minutes to cool in a room having a temperature of 25°C. The graph above shows the temperature of each sample at 10-minute intervals. Which of the following statements correctly compares the average rates at which the temperatures of the two samples change?View SolutionC=59(F−32)
The equation above shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.View Solution

