Two projectile are projected simultaneously from a point on the ground "O" and an elevated position "A" respectively as shown in the figure. If collision occurs at the point of return of two projectiles on the horizontal surface, then find the height of "A" above the ground and the angle at which the projectile "O" at the ground should be projected.
Text Solution
There is no initial separation between two projectile is x-direction. For collision to occur, the relative motion in x-direction should be zero. In other words, the component velocities in x-direction should be equal to that two projetiles cover equal horizontal distance at any given time. Hence,
uOx=u(Ax)
⇒u0cosθ=uA
⇒cosθ=uAu0=510=12=cos60∘
⇒θ=60∘
We should ensure that collision does occur at the point of return. It means that by the time projectiles travel horizontal distances required, they should also cover vertical distances so that both projectile areat "C" at the same time. In the nutshell, their times of flight should be equal. For projectile from "O"
T=2uOsinθg
For projectile from "A",
T=√2Hg
For projectile from " A"
T=2u0sinθg=√(2Hg)
Squaring both sides and putting values,
⇒H=4u2Osin2θ2g
⇒H=4×102sin260∘2×10
H=20(√32)2=15m
We have deliberately worked out this problem taking advantage of the fact that projectiles are colliding at the end of their flights and hence their times of flight should be equal. We can, however, proceed to analyze in typical manner, using concept of relative velocity. The initial separation between two projectiles in the vertical direction is "H". This separation is covered with the component of relative in vertical direction.
⇒vOAy=uOy−uAy=uBsin60∘−0=10×√32
=5√3m/s
Now, time of flight of projectile from ground is :
T=2u0sinθg=2×10×sin60∘10=√3
Hence, the vertical displacement of projectile from "A" before collision is :
⇒H=vOAyXT=5√3x√3=15m/s
|
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
Knowledge Check
Find the angle of projection of a projectile for which the horizontal range and maximum height are equal.
Aα=tan−1(2)Bα=tan−1(4)Cα=tan−1(5)DNone of the aboveReferring to above question, the angle with the horizontal at which the projectile was projected is
Atan−1(3/4)Btan−1(4/3)Csin−1(3/4)DNot obtainable from the dataThe angle of projection at which the horizontal range and maximum height of projectile are equal is
A45∘Bθ=tan−1(0.25)Cθ=tan−1(4)D60∘
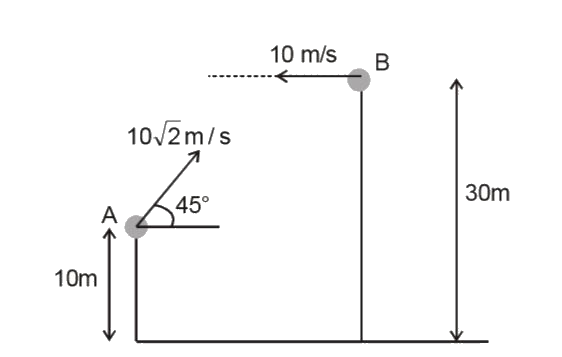
Two projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
View SolutionWhich of the following is the graph between the height (h) of a projectile and time (t), when it is projected from the ground
View SolutionWhich of the following is the graph between the height (h) of a projectile and time (t), when it is projected from the ground
View SolutionThe horizontal range is equal to two times maximum height of a projectile. The angle of projection ofthe projectile is:
View SolutionA projectile is hurled into air from a point on the horizontal ground at an angle with the vertical. If the air exerts a constat resistve force,
View Solution
