A thin disc of mass M and radius R has mass per unit area σ(r)=kr2, where r is the distnace from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is xMR2, where x is _________
The correct Answer is:0.67
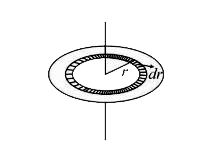
Disc can be understood as the combination of co-axial rings.
M.I. of element ring of radius r and infinitesimally small thickness dr about the axis is
dI=(dm).r2={(kr2)2πrdr}r2
⇒I=2πkR6/6 ...........(1)
Also, mass of ring, M=∫dm=∫Rr=0(kr2)(2πrdr)
Or, M=2πkR44........(2)
From (2) and (2)
I=46MR2=23MR2
Similar Questions
A thin disc of mass M and radius R has mass per unit area σ(r)=kr2 where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is : a) MR33 b) 2MR23 c) MR26 d) MR22
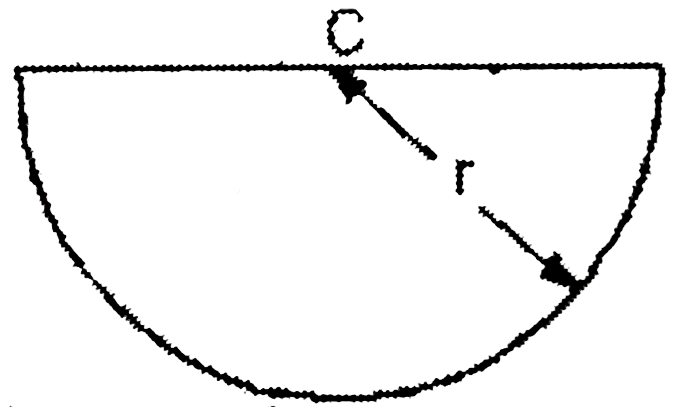
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View Solution
Knowledge Check
A thin disc of mass M and radius R has mass per unit area σ(r)=kx2 where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is:
AMR23B2MR23CMR26DMR22A semicircular lamina of mass m and radius 'r' and centre C. Its center of mass is at a distance 'x' from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
 A12mr2B14mr2C12mr2+mx2D12mr2−mx2
A12mr2B14mr2C12mr2+mx2D12mr2−mx2A solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
A2MR23+MI212BMR23+MI212C3MR23+MI212DMR24+MI212
Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution
