A platform P is moving with a velocity $v_{P}$ over hemispherical shell. A vertical rod AB passing trhough a hole in the platform is moving on the shell and remains vertical. There is sufficient friction between rod and shell to stop the slip. C is the crown of the shell and O is its cenre $∠ B O C = θ$ at any instant. find the velocity of point B in downward motion at that instnat:

A

$u_{p} sin θ$

B

$u_{p} cos θ$

C

$u_{p} tan θ$

D

$u_{p} cot θ$

Text Solution

Verified by Experts

The correct Answer is:c

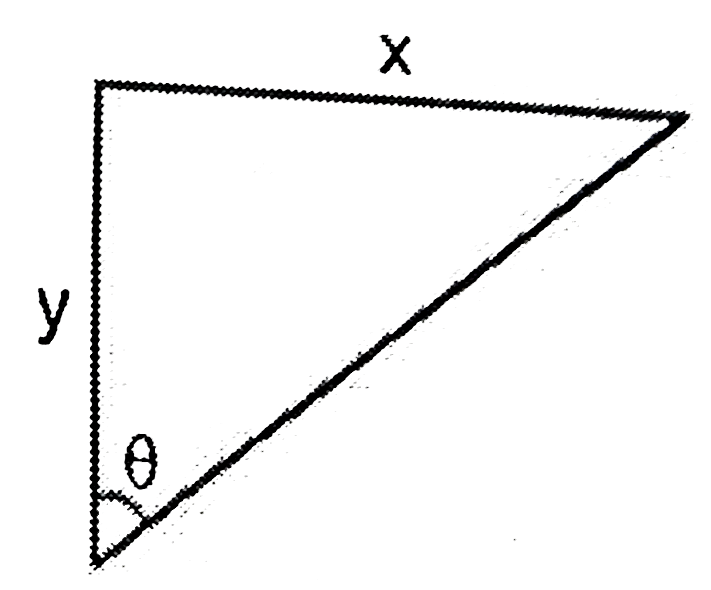
$\frac{x}{y} = tan θ$
$x = y tan θ$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the previous problem, the velocity of the shell will be
A $30 m s^{- 1}$
B $30 \sqrt{2} m s^{- 1}$
C $30 \sqrt{3} m s^{- 1}$
Dnone of these
Question 2 - Select One
A thin non-conducting hemispherical shell contains a positive charge $q$ on it, which uniformly distributed on the shell. A point $P$ lies on the diameter of shell as show in figure. Then the direction of electric field at the point $' P'$ is

A
B
C
D
Question 3 - Select One
A vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is $θ$ . The induced e.m.f. in the rod is
A $B l v sin θ$
B $B l v tan θ$
C $B l v cot θ$
D $B l v cos θ$

GRB PUBLICATION-MOTION IN TWO AND THREE DIMENSIONS-All Questions

Home
Ask Doubt
Profile