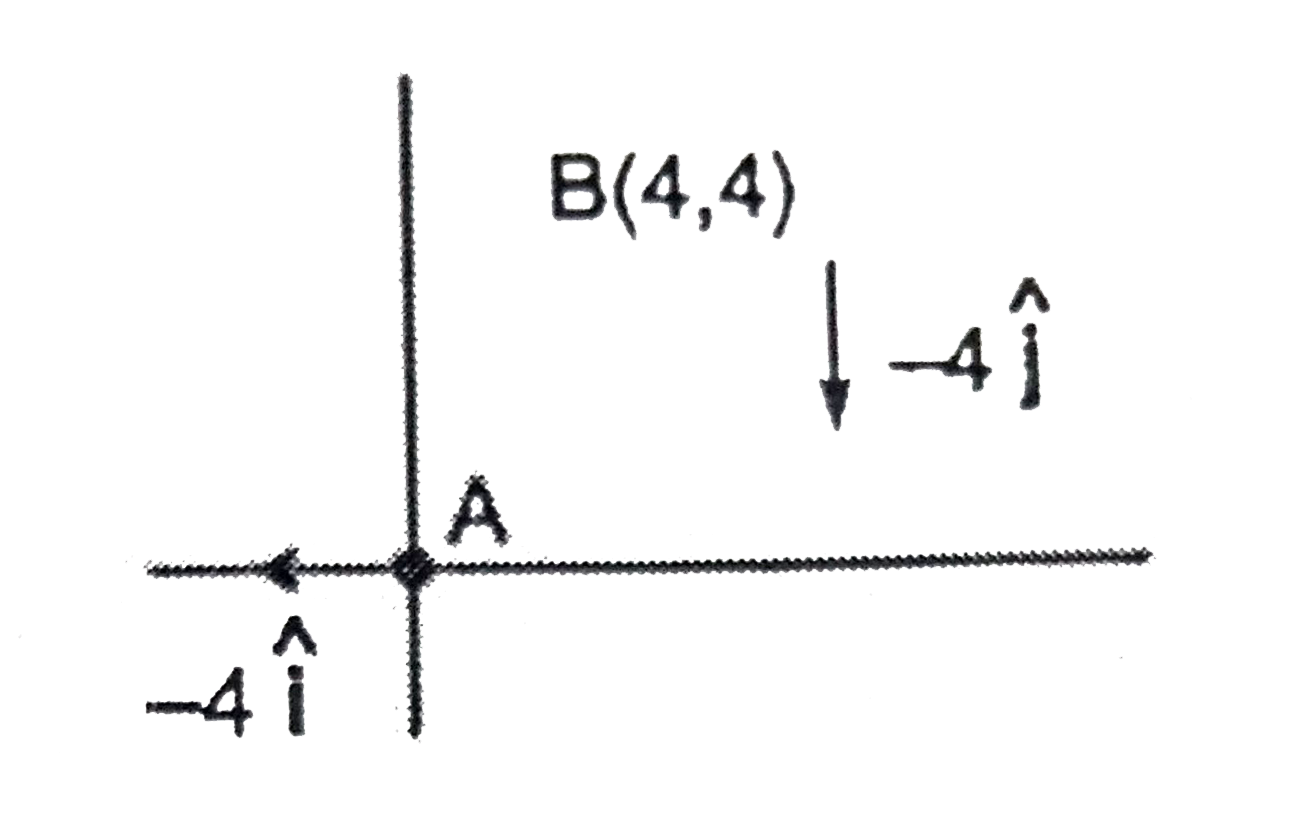
Two particles A and B locat at (0,0) and (4,4) respectively start moving simu lataneou ly with velocities vA=−4ˆi and VB=−4ˆj:
the shortest distance between them is 4√2m
the shortest distance between them first decreases and then increases
the distance between them increases from the beginning
the magnitude of relative velocity of A w.r.t. B is 4m/s
The correct Answer is:a,c
The shortest distane h/w them is
AB=4√2m
Because the distance b/w them increases from start.
Topper's Solved these Questions
Similar Questions
Two particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
View SolutionTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two projectile A and B located at (0,0) and (4.4) respectively start moving simu ltaneou lsy with velocities VA=−4ˆi and VB=4ˆj:
Athe shortest distance between them is 4√2mBthe shortest distance between them first decreases and then increasesCthe distance between them increases from the beginningDthe magnitude of relative velocity of A w.r.t. B is 4m/s - Question 2 - Select One or More
Two particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
Athe distance between them is constantBThe distance between them first decreases and then increasesCthe shortest distance between them is 2√2mDTime after which they are at minimum distances is 1s - Question 3 - Select One
Two particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then
 Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
A flat rigid body is moving in x–y plane on a table. The plane of the body lies in the x–y plane. At an instant it was found that some of the velocity components of its three particles A, B and C were VAx=4m/s,VBx=3m/s and Vcy=−2m/s, respectively. At the instant the three particles A, B and C were located at (0,0) (3,4) , (4,3) (all in meter ) respectively in a co-ordinate system attached to the table.
(a) Find the velocity of A, B and C
(b) Find the angular velocity of the body.
 View Solution
View SolutionTwo particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionA body of mass m1 moving with an unknown velocity of v1ˆi, undergoes a collinear collision with a body of mass m2 moving with a velocity v2ˆi. After collision , m1 and m2 move with velocities of v3ˆi and V4ˆi , respectively. If m2=0.5m1 and v3=0.5v1, then v1 is :
View SolutionTwo particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionA particle moving with a velocity of (4ˆi−ˆj ) mis strikes a fixed smooth wall and finally moves with a velocity of (3ˆi+2ˆj) m/s. The coefficient of restitution between the wall and the particle in the collision will be
View Solution

