Two blocks of masses m1=5 kg and m2=2 kg are connected by threads which pass over the pulleys as shown in the figure. The threads are massless and the pulleys are massless and smooth. The blocks can move only along the vertical direction T1andT2 are the tensions in the string as shown. Now match the following: (Takeg=10m/s2)

Column -IColumn -II(a)Magnitude value ofacceleration of m1 with respect to ground(p)50019SI units(b)Magnitude value ofacceleration ofm2with respect to ground(q)25019SI units(c)The value of tensionT1(r)6019SI units(d)The value of tensionT2(s)4019SI units(t)None of the above
The correct Answer is:a→s;b→r;c→q;d→p
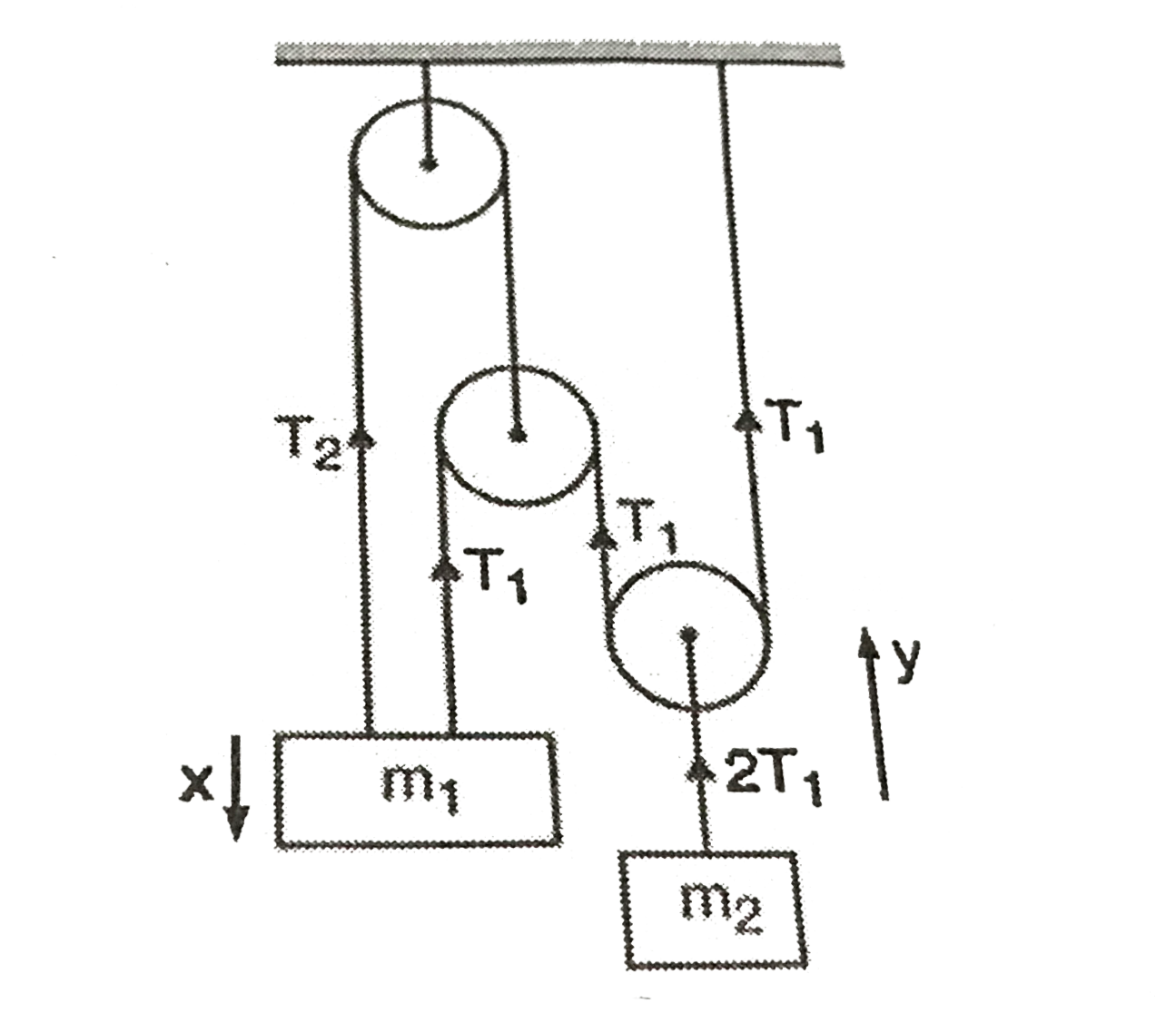
T2=2T1
Now, m1g−T1−T2=m1a1
2T1−m2g=m2a2 ...(ii)
as y=(3x2)
2a2=3a1….(iii)
By solving we will get the answer a1=(4019)m/sec2
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Integer question
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
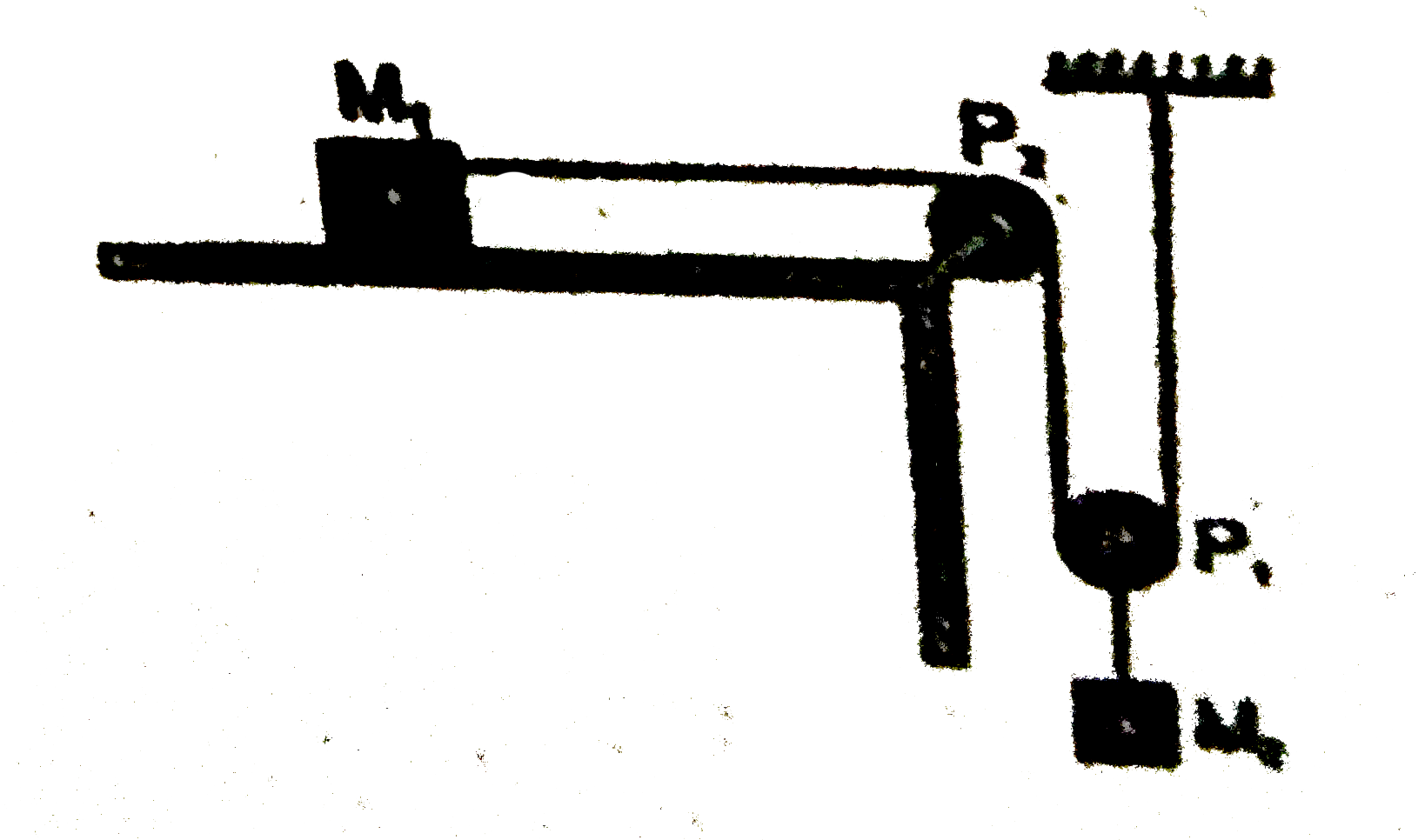
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View Solution
Knowledge Check
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
 AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)
AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)Two blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 A27 NB54 NC0.8 NDZero
A27 NB54 NC0.8 NDZeroTwo blocks of masses mi=2kg and m2=4kg hang, over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards Then :
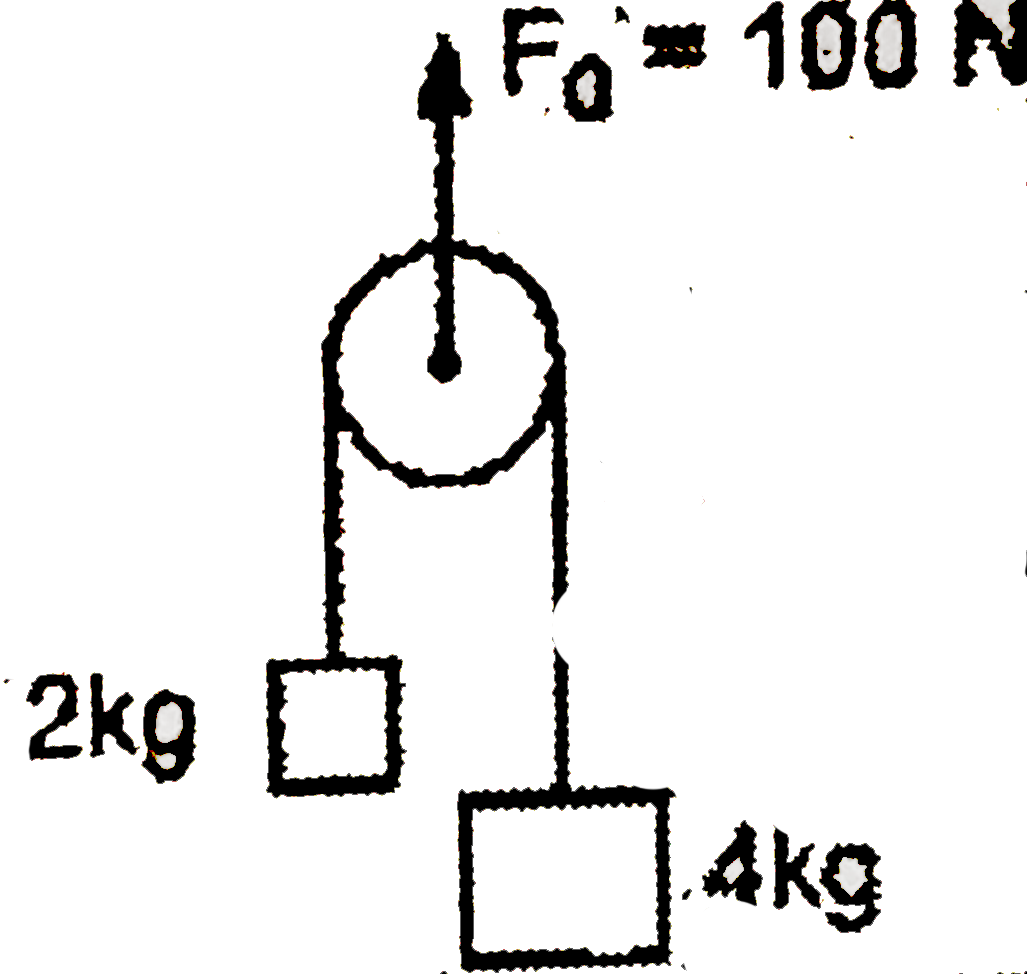 Aacceleration of 2kg mass is 15m/s2Bacceleration of 4kg mass is 2.5m/s2Cacceleration of both masses is sameDacceleration of both the masses is upward
Aacceleration of 2kg mass is 15m/s2Bacceleration of 4kg mass is 2.5m/s2Cacceleration of both masses is sameDacceleration of both the masses is upward
Two blocks of masses m1=2kg and m2=5kg hang over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards. Then :( Take g=9.8m/s2)

View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
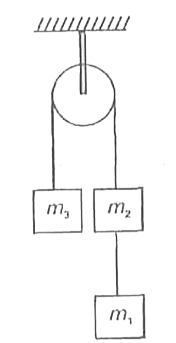
View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)

View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1=2kg and m2=5kg hang over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards. Then :( Take g=9.8m/s2)

View Solution
