A block of mass m is kept on a smooth moving wedge If the acceleration of the wedge is equal to a, then match the following:
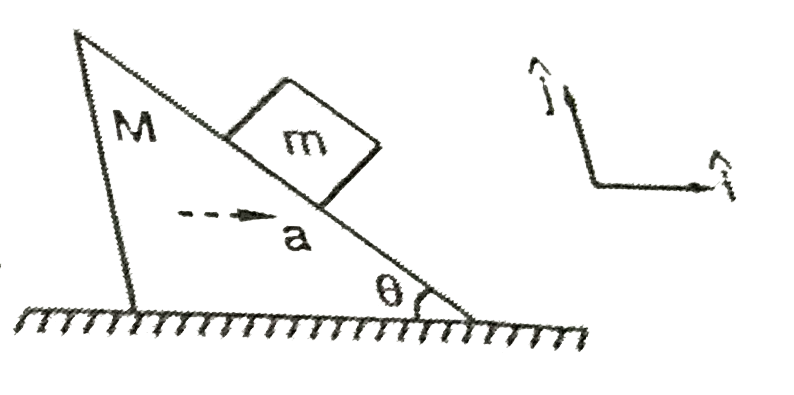
Column -IColumn -II(a)Acceleration of m(p)Ma+m(gcosθ+asinθ)sinθ(b)Acceleration of mrelative to the wedge(q)(gsinθ−acosθ)(c)Force on the wedgeexerted by ground(r)(√g2+a2)sinθ(d)Force on the wedgeexerted by external agent(s)(M+mcos2θ)g+masinθcosθ
The correct Answer is:a→r;b→q;c→s;d→p
From the fig

ar=gsinθ−acosθ
∴(b)→(q)
anet=√a2+a2r+2a(ar)cosθ
=√a2+(gsinθ−acosθ)2+2a(gsinθ−acosθ)cosθ
=√a2+g2sin2θ+a2cos2θ−2gasinθcosθ
+2gasinθcosθ−2a2cos2θ
=√a2+g2sin2θ−a2cos2θ
=(√a2+g2)sinθ
∴(a)→(r)
(c) Also, N=mgcosθ+masinθ
∴N1=Mg+Ncosθ
=Mg(mgcosθ+masinθ)cosθ
=Mg+mgcos2θ+masinθcosθ
∴(c)→(s)
(d) Fext−Nsinθ=Ma
Fext=Ma+(mgcosθ+masinθ)sinθ
=Ma+mgsinθcosθ+masin2θ
∴(d)→(p)

Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Integer question
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
Block of mass m is sliding up on the smooth inclined plane with some initial velocity Now on the block match the magnitude value of the forced on 'm' in the given directions (take the component of all the forces in the given direction)

Column -IColumn -II(a)Net force component inhorizontal direction(p) Zero(b)Net force component invertical direction(q)mgsinθcosθ(c)Net force componentalong the inclined plane(r)mgsinθ(d)Net force componentpenpendicular to the inclined plane(s)mg(1−cos2θ)
View Solutionif (2m+1)sinθ=2m(m+1)cosθ, then sinθ=
View Solution
Knowledge Check
If sinθ,1,cos2θ are in G.P. , then θ =
Anπ+(−1)nπ2Bnπ+(−1)n−1π2C2nπDnoneA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθA block of mass m is placed on a smooth wedge of wedge angle θ The whole system is accelerated horizontally so that the block does not slip on the wedge. The force (normal reaction) exerted by the wedge on the block has a magnitude:
AmgtanθBmgcosθCmgDmgcosθ
A block of mass m is placed on a smooth wedge of inclination θ. The while system is acceleration horizontally so that the block does not slip. Find (a) horizontal acceleration, (b) normal force between the block and the wedge and (c) the horizontal force applied on the wedge.
View SolutionA block of mass m is thrown upwards with some initial velocity as shown in figure. On the block
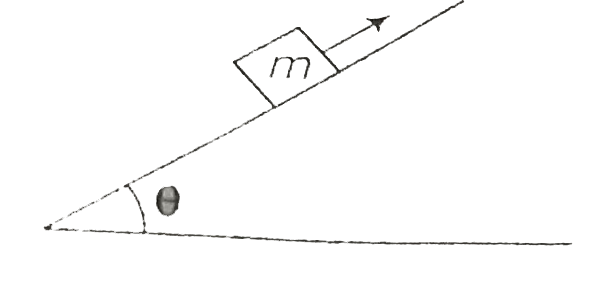
Column IColumn II(A) Net force in horizontal direction(p) Zero(B) Net force in vertical direction(q)m(gsinθ+μgcosθ)(C) Net force along the plane(r)m(gsinθcosθ+μgcos2θ)(D) Net force perpendicular to plane(s)m(gsin2θ+μgsinθcosθ)
View SolutionA block of mass m is thrown upwards with some initial velocity as shown in figure. On the block

Column IColumn II(A) Net force in horizontal direction(p) Zero(B) Net force in vertical direction(q)m(gsinθ+μgcosθ)(C) Net force along the plane(r)m(gsinθcosθ+μgcos2θ)(D) Net force perpendicular to plane(s)m(gsin2θ+μgsinθcosθ)
View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

View Solution
