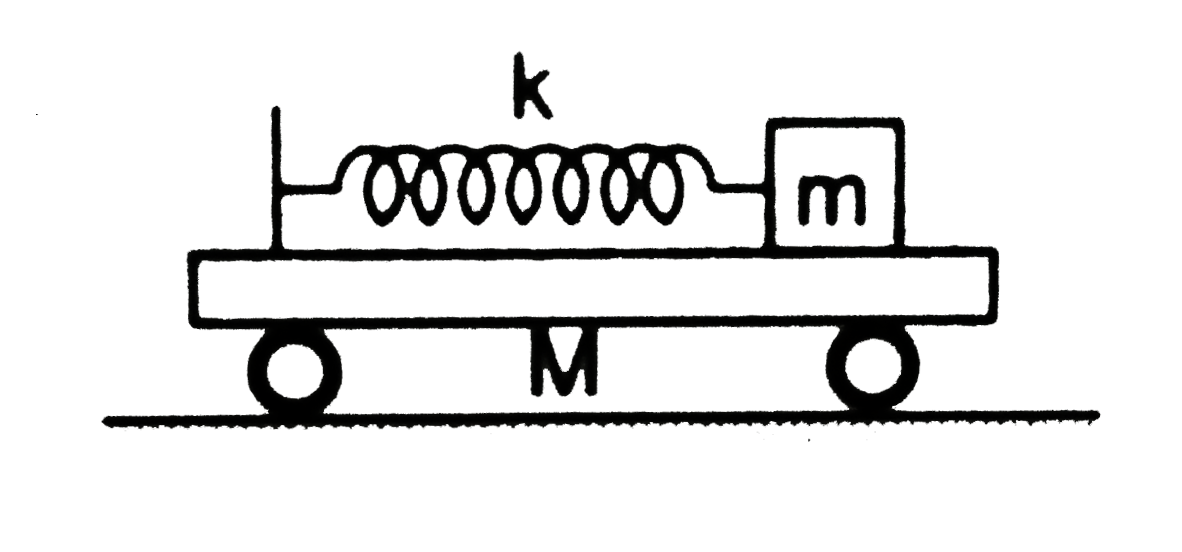
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the blcok. Find the amplitude and the frequency of the motion of the block.
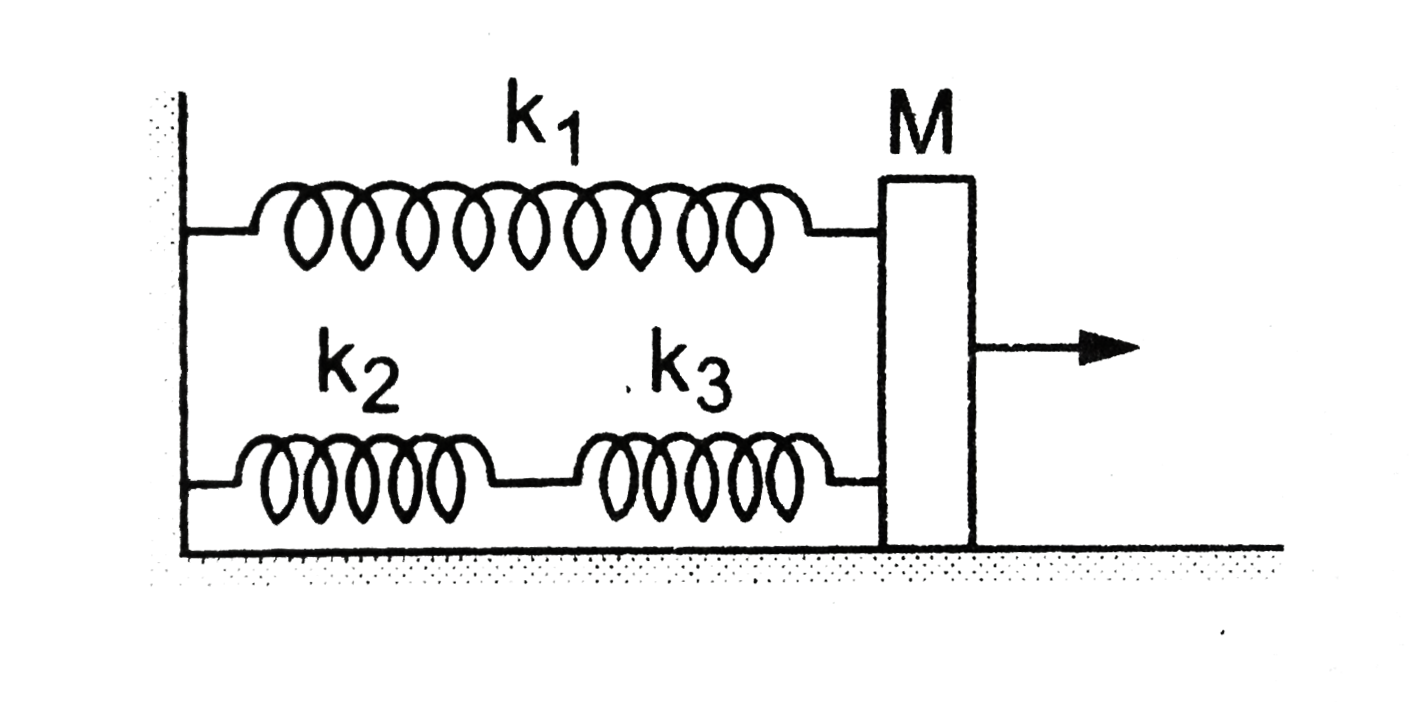
F(K2+K3)K1K2+K2K3+K3K1,12π√K1K2+K2K3+K3K1M(K2+K3)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-I) ( SECTION - E,F ) ( Angu lar shm & s imple pendulum )2videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-I) ( SECTION - G ) (Compound pendulum / physicalpendulum, torsional pendulum )1videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-I) ( SECTION - C ) ( Two block system )2videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)14videos
SOUND WAVES
Similar Questions
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.View SolutionA spring mass systeam is shown in figure, spring is initially unstretched. A man starts pulling the block with constant force F. Find
(a) The amplitude and the time period of motion of the block
(b) The K.E. of the block at mean position
(c) The energy stored in the spring when the block passes through the mean position
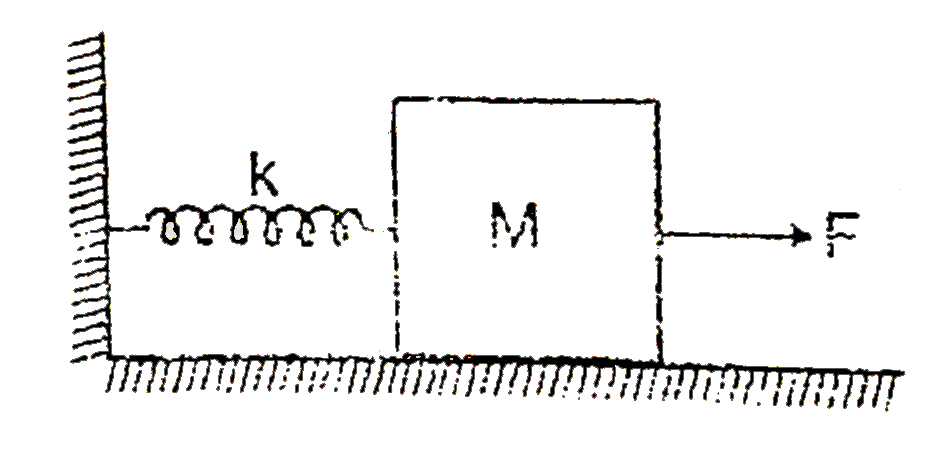 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
The springs shown in the figure are all upstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block.
 Athe amplitude of oscillation is (K2+K3)FK1K2+K2K3+K3K1Bthe oscillation frequency is 12π[K1K2+K2K3+K3K1M(K2+K3)]1/2Cthe amplitude of oscillation is 2(K2+K3)FK1K2+K2K3+K3K1Dthe oscillation frequency is 1π[K1K2+K2K3+K3K1M(K2+K3)]1/2
Athe amplitude of oscillation is (K2+K3)FK1K2+K2K3+K3K1Bthe oscillation frequency is 12π[K1K2+K2K3+K3K1M(K2+K3)]1/2Cthe amplitude of oscillation is 2(K2+K3)FK1K2+K2K3+K3K1Dthe oscillation frequency is 1π[K1K2+K2K3+K3K1M(K2+K3)]1/2 - Question 2 - Select One
A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
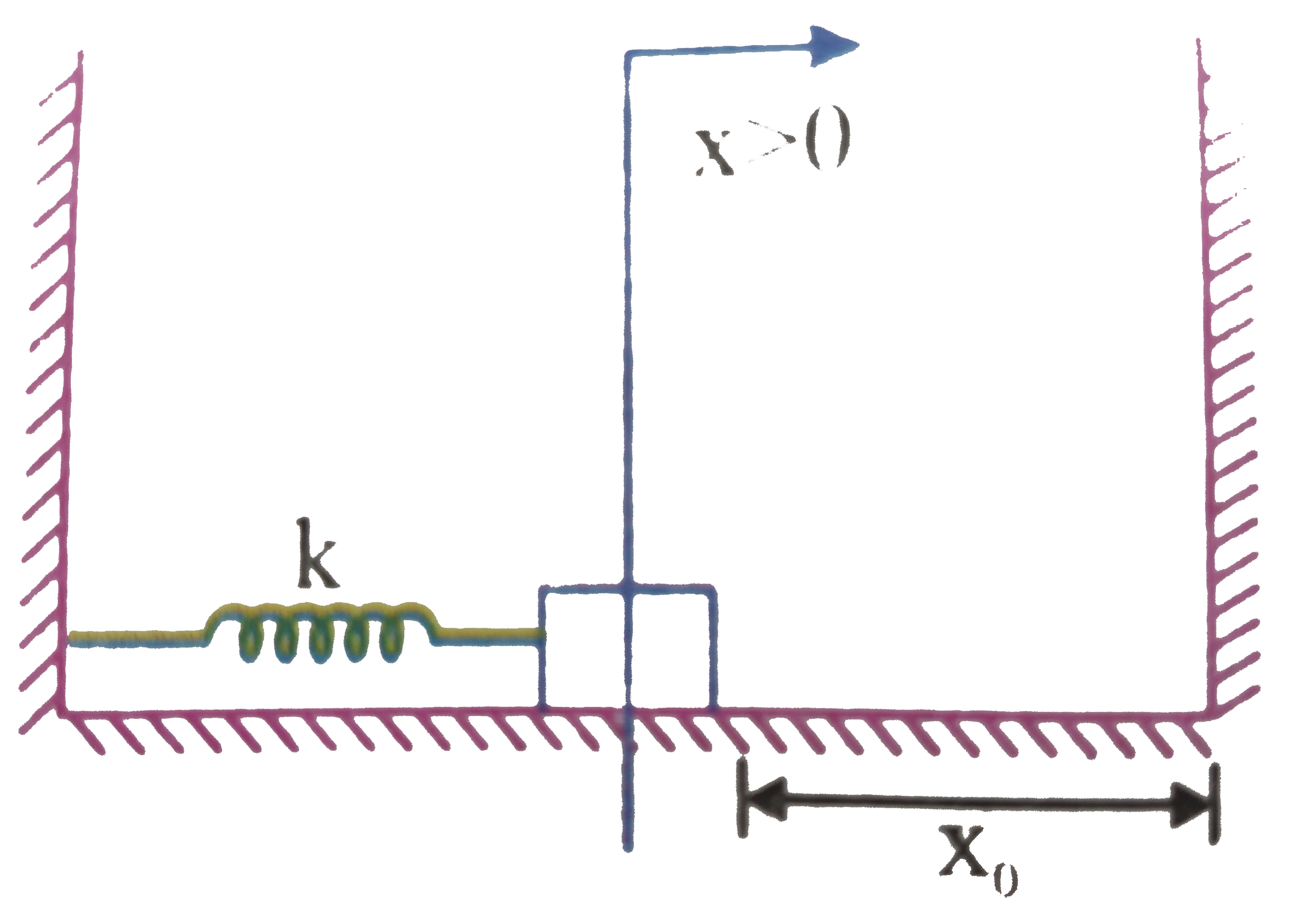
Find the time period of motion of the block:A2π3√mkB4π3√mkC3π2√mkDπ2√mk - Question 3 - Select One
A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)
As shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View Solution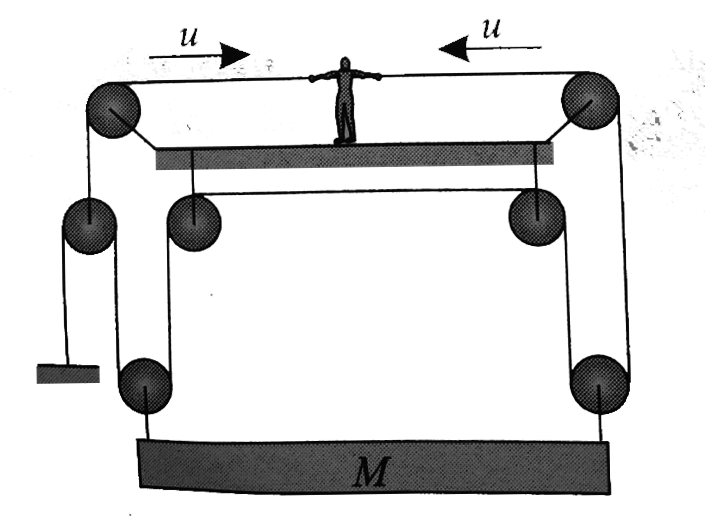
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.View SolutionAll the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
 View Solution
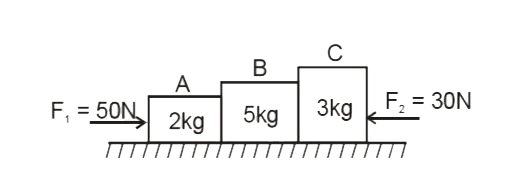
View SolutionFind the contact force between the block and acceleration of the blocks as shown in figure.
 View Solution
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View Solution

