In an acute angle triangle ABC, AD, BE and CF are the altitudes, then EFa+FDb+DEc is equal to -
Step by step video & image solution for In an acute angle triangle ABC, AD, BE and CF are the altitudes, then (EF)/a+(FD)/b+(DE)/c is equal to - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In ΔABC and ΔDEF , AB = DE, AB∣∣DE, BC = EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
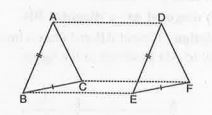 Show that AD∣∣CF and AD=CF.
Show that AD∣∣CF and AD=CF.
View SolutionIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
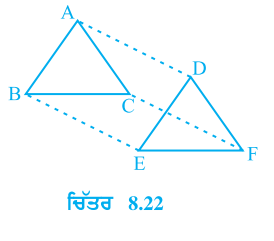
View Solution△ABC ਅਤੇ △DEF ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- AD || CF ਅਤੇ AD = CF ਹੈ।
View SolutionIn an acute angled triangle ABC, let AD,BE and CF be the perpendicular opposite sides of the triangle. The ratio of the product of the side lengths of the triangles DEF and ABC, is equal to
View SolutionIn an acute angle triangle ABC, AD, BE and CF are the altitudes, then EFa+FDb+DEc is equal to -
View SolutionIn an acute angle triangle ABC, AD, BE and CF are the altitudes, then EFa+FDb+DEc is equal to -
View SolutionIn ΔABC and ΔDEF , AB = DE, AB∣∣DE, BC = EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that AD∣∣CF and AD=CF.
Show that AD∣∣CF and AD=CF.
View SolutionConsider an acute angled Delta ABC. Let AD, BE and CF be the altitudes drawn from the vertice to the opposite sides. Prove that : (EF)/(a)+ (FD)/(b)+ (DE)/(c)= (R+r)/(R ).
View Solution
