Find min velocity v0 such that particle cross the ring.
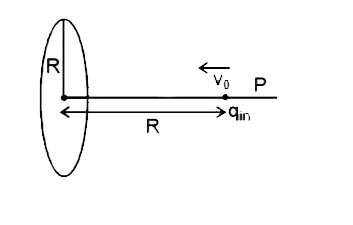
Potential at P=kQ√2R
Applying energy conservation
12mv20+kQq√2R=0+kqQR
⇒v0
⎷2kQqmR(1−1√2)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)10videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)10videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main30videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)30videos
ELECTROSTATICS-II
Similar Questions
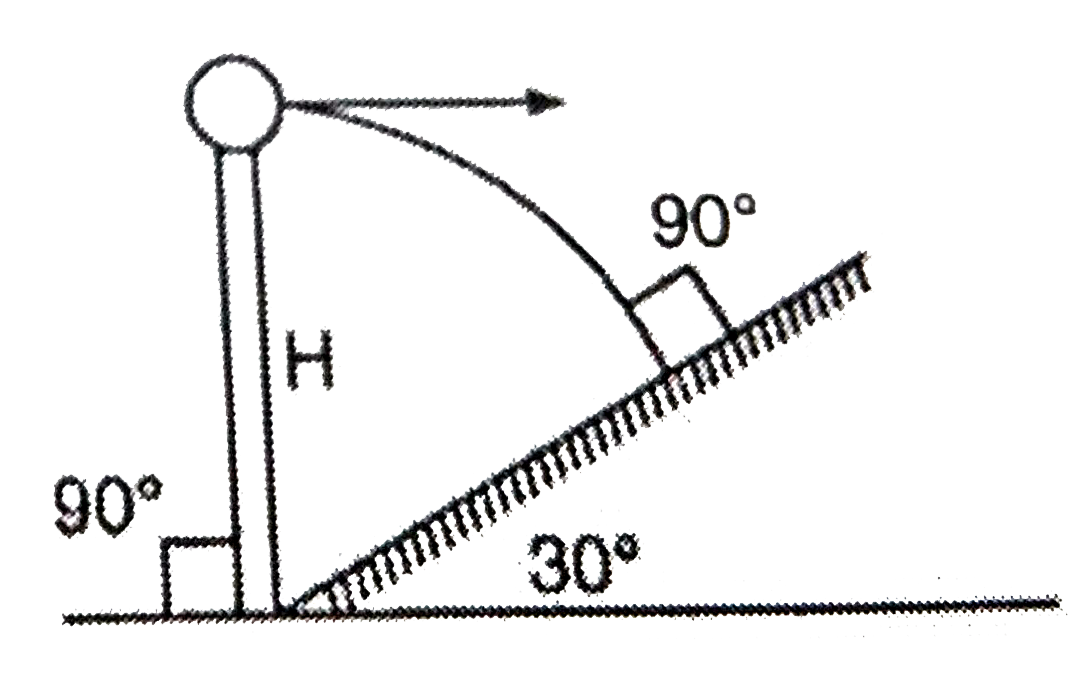
In the given figure , the angle of inclination of the inclined plane is 30∘. A particle is projected with horizontal velocity v0 from height H. Find the horizotnal velocity v0 (in m/s) so that the particle hits the inclined plane perpendicu lar .Given H=4m, g=10m/s2.
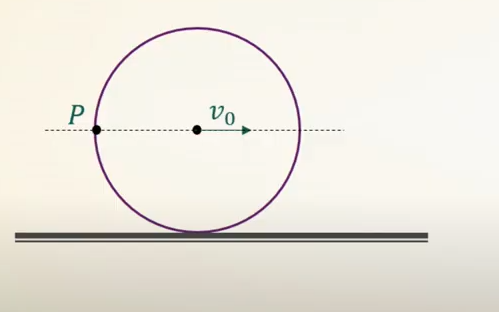
View SolutionThe centre of the wheel rolling on a plane surface moves with velocity v0. A particle on the rim of the wheel at same level as the centre will be √xv0. Find x
View Solution
Knowledge Check
- Question 1 - Select One
In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
. AV0=√2gH5BV0=√2gH7CV0=√gH5DV0=√gH7 - Question 2 - Select One
A particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
Av=v0/(1+kv0t)Bv=2v01+ktCv=v0ktDv=v0(1+k2v02t)
The velocity components of a particle moving in the xy plane of the reference frame K are equal to vx and vy. Find the velocity v′ of this particle in the frame K in the positive direction of its x axis.
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA positively charged particle is given an initial velocity v0 in XY plane as shown in diagram. Initially the particle was at origin and the region contains uniform, mutually perpendicular electric and magnetic field. Let →E=−Eˆj and →B=Bˆk. The minimum magnitude of the magnetic field so that the charge particle crosses the origin again during its subsequenty motion is Bmin=nπEv0, find the integer value n
View Solution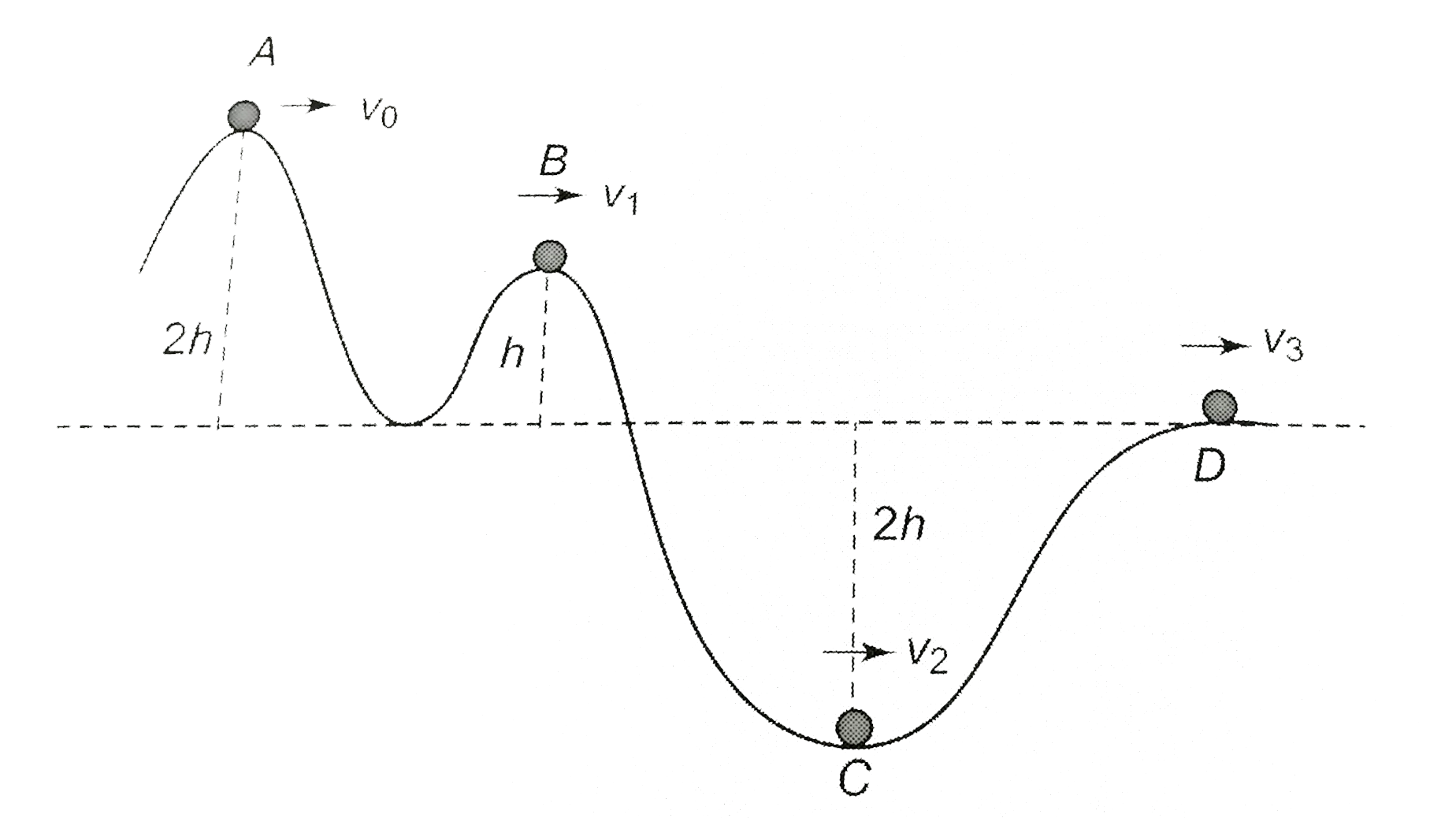
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionReferring a−s diagram in , find the velocity after particle travel 120m from starting. Assume v0=0.
.View SolutionA particle of mass 1.0g moving with velocity v1=3.0i−2.0j experiences a perfectly inelastic collision with another particle of mass 2.0g and velocity v2=4.0j−6.0k. Find the velocity of the formed particle (both the vector v and its modulus), if the components of the vectors v1 and v2 are given in the SI units.
View Solution