The centre of the wheel rolling on a plane surface moves with velocity v0. A particle on the rim of the wheel at same level as the centre will be √xv0. Find x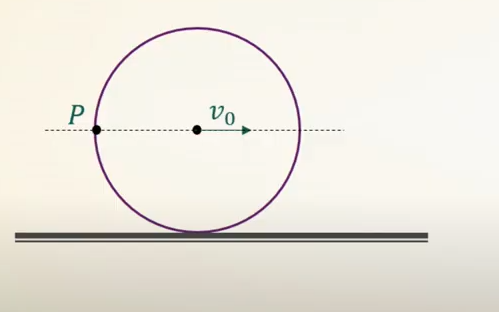 
√2
2
3
4
Step by step video & image solution for The centre of the wheel rolling on a plane surface moves with velocity v_0. A particle on the rim of the wheel at same level as the centre will be sqrt(x)v_0. Find x by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The centre of a wheel rolling on a plane surface moves with a speed v0 . A particle on the rim of the wheel at the same level as the centre will be moving at a speed √xv0 . Then the value of x is ______ .
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View Solution
Knowledge Check
- Question 1 - Select One
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0 - Question 2 - Select One
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0 - Question 3 - Select One
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0
Find min velocity v0 such that particle cross the ring.
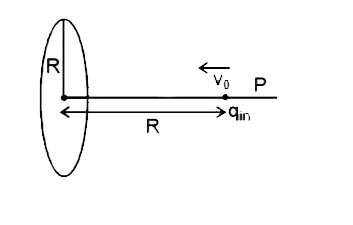
View SolutionEscape velocity for a projectile at the earth's surface is ve+ A body is projected from the earth's surface with velocity 2ˆve+. The velocity of the body when it is at infinite distance from the centre of the earth is √xve. Find x
View SolutionTwo thin rings of slightly different radii are joined together to make a wheel (see figure) of radius R. There is a very small smooth gap between the two ring. The wheel has a mass M and its centre of mass is at its geometrical centre. The wheel stands on a smooth surface and a small particle of mass m lies at the top (A) in the gap between the rings. The system is released and the particle begins to slide down along the gap. Assume that the ring does not lose contact with the surface.
(a) As the particle slides down from top point A to the bottom point B, in which direction does the centre of the wheel move?
(b) Find the speed of centre of the wheel when the particle just reaches the bottom point B. How much force the particle is exerting on the wheel at this instant?
(c) Find the speed of the centre of the wheel at the moment the position vector of the particle with respect to the centre of the wheel makes an angle q with the vertical. Do this calculation assuming that the particle is in contact with the inner ring at desired value of θView SolutionA sphere of mass m rolls on a plane surface.Find its kinetic energy t an instant when its centre moves with speed v.
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View Solution