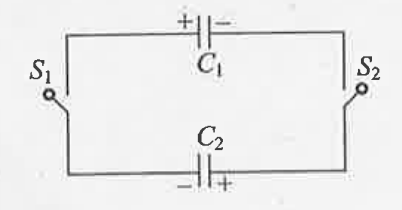
Two capacitorsC1=4μFandC2=2μF are charged to same potential V = 500 Volt, but with opposite polarity as shown in the figure. The switches S1andS2are closed.
The potential difference across the two capacitors are same and is given by 500/3V
The potential difference across the two capacitors are same and is given by 1000/3V
The ratio of final energy to initial energy of the system is 1/9
The ratio of final energy to initial energy of the system is 4/9
The correct Answer is:A, C
Topper's Solved these Questions
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -3 LEVEL 1
31 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -3 LEVEL II
17 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -2
36 Videos
- CALORIMETRY BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B
4 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
Similar Questions
Two capacitors C1=4μFandC2=2μF are charged to same potential V = 500 Volt, but with opposite polarity as shown in the figure. The switches S1andS2 are closed.

View SolutionTwo capacitors C1 and C2 are charged to same potential V, but with opposite polarity as shown in the figure. The switches S1 and S2 are then closed

View Solution
Knowledge Check
Two capacitors C1=2μF and C2=1μF are charged to same potential V=100V, but with opposite polarity as shown in the figure.
The switches S1 and S2 are closed. The ratio of final energy to the initial energy of the system is
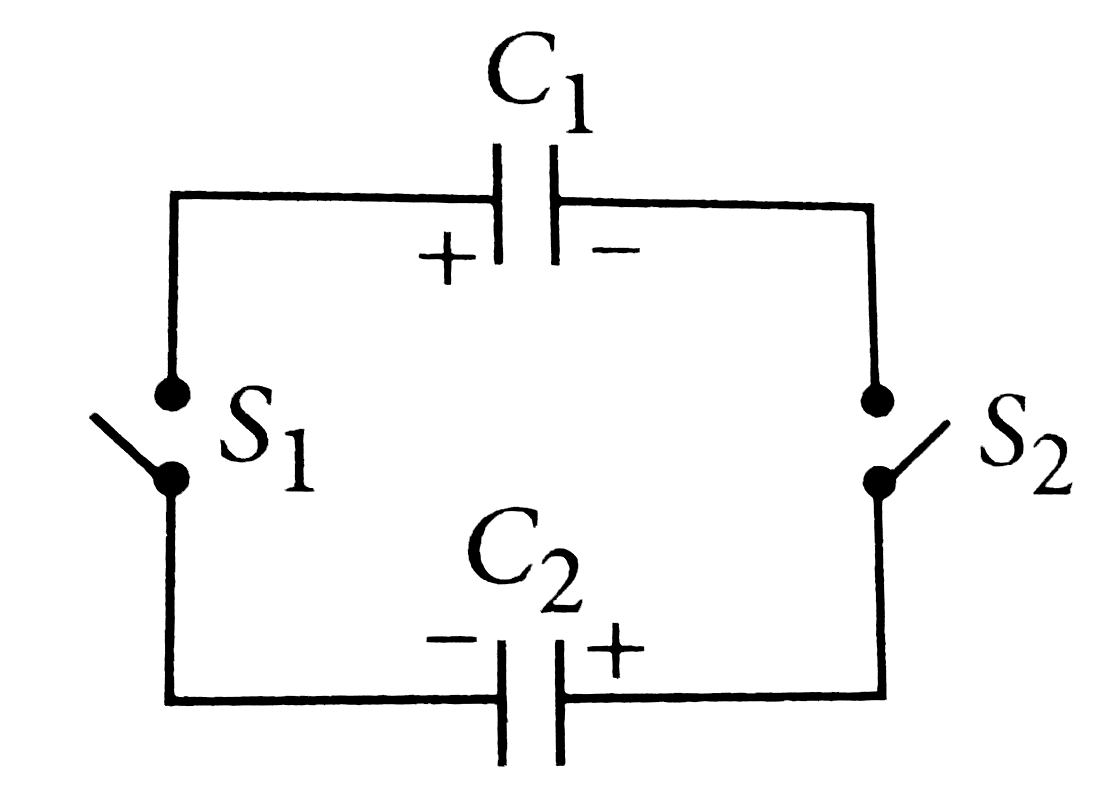 A1B12C19D14
A1B12C19D14Two capacitors C1=2μF and C2=1μF are charged to same potential V=100V, but with opposite polarity as shown in the figure.
The switches S1 and S2 are closed. The ratio of final energy to the initial energy of the system is
 A1B12C19D14
A1B12C19D14Two capacitors C1 and C2 are charged to same potential V, but with opposite polarity as shown in the figure. The switches S1 and S2 are then closed
 APotential difference across two capacitors are same and is given by (C1−C2)VC1+C2BPotential difference across two capacitors are same and is given by (C1+C2C1−C2)VCRatio of final energy to initial energy of the system is given by (C1−C2)2(C1+C2)2DRatio of final energy to initial energy of the system is given by (C1)2(C1+C2)2
APotential difference across two capacitors are same and is given by (C1−C2)VC1+C2BPotential difference across two capacitors are same and is given by (C1+C2C1−C2)VCRatio of final energy to initial energy of the system is given by (C1−C2)2(C1+C2)2DRatio of final energy to initial energy of the system is given by (C1)2(C1+C2)2
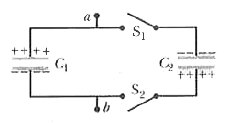
Two capacitors C1=1μF and C2=3μF each are charged to a potential difference of 100V but with opposite polarity as shown in the figure. When the switch S is closed, the new potential difference between the points a and b is
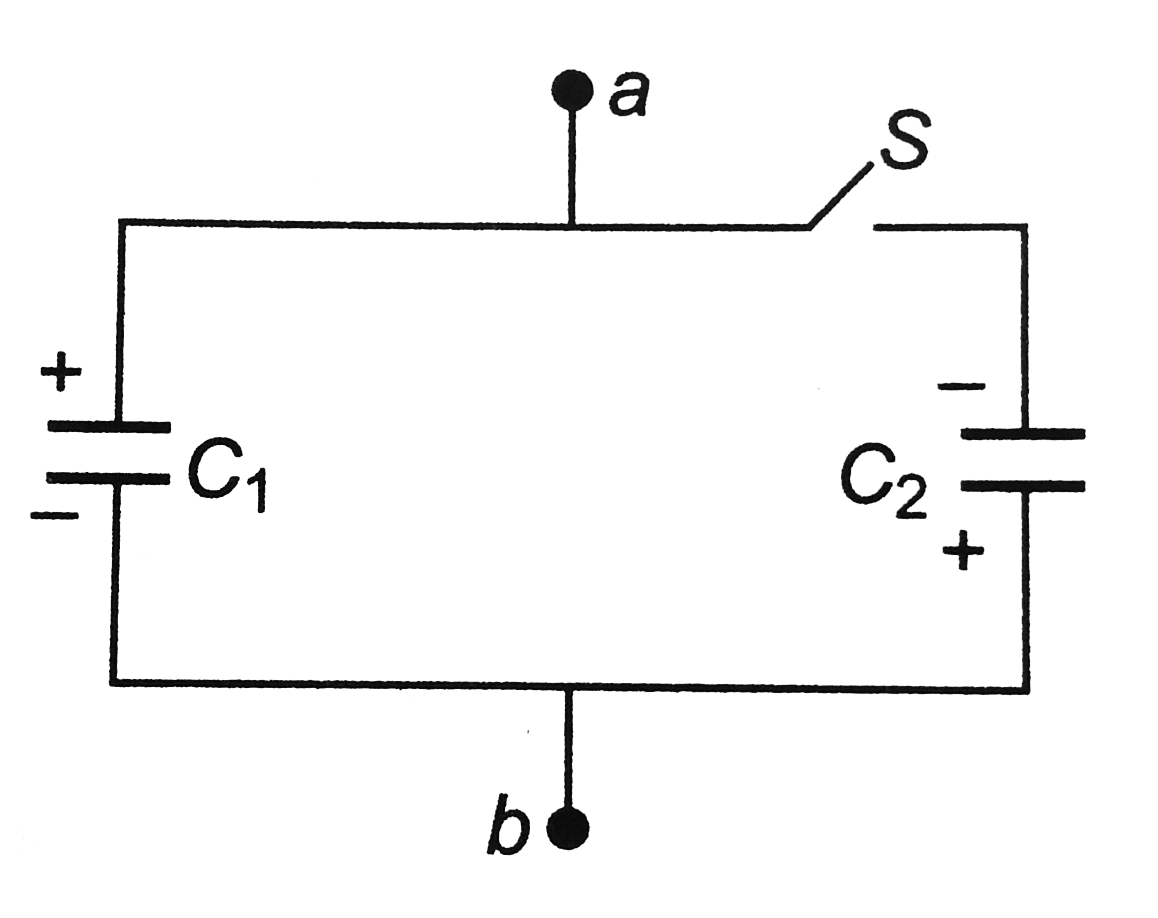
View SolutionIn fig 25-39 the capacitances are C1=1.0μFandC2=3.0μF and both capacitors are charged to a potential difference of V=200V but with opposite polarity as shown. Switches S1andS2 are now closed. (a) What is the now the potential difference between points a and b? What now is the charge on capacitor (b) 1 and (c) 2?
View SolutionTwo capacitors C1andC2 are charged to the same potential V, but with opposite polarity as shown in the figure. The switch S1andS2 are then closed.
View SolutionTwo capacitors C1=1μF and C2=3μF each are charged to a potential difference of 100V but with opposite polarity as shown in the figure. When the switch S is closed, the new potential difference between the points a and b is

View SolutionTwo capacitor of capacity 6μF and 3μF are charged to 100 V and 50 V separately and connected as shown in figure. Now all the three switches S1,S2,andS3 are closed.
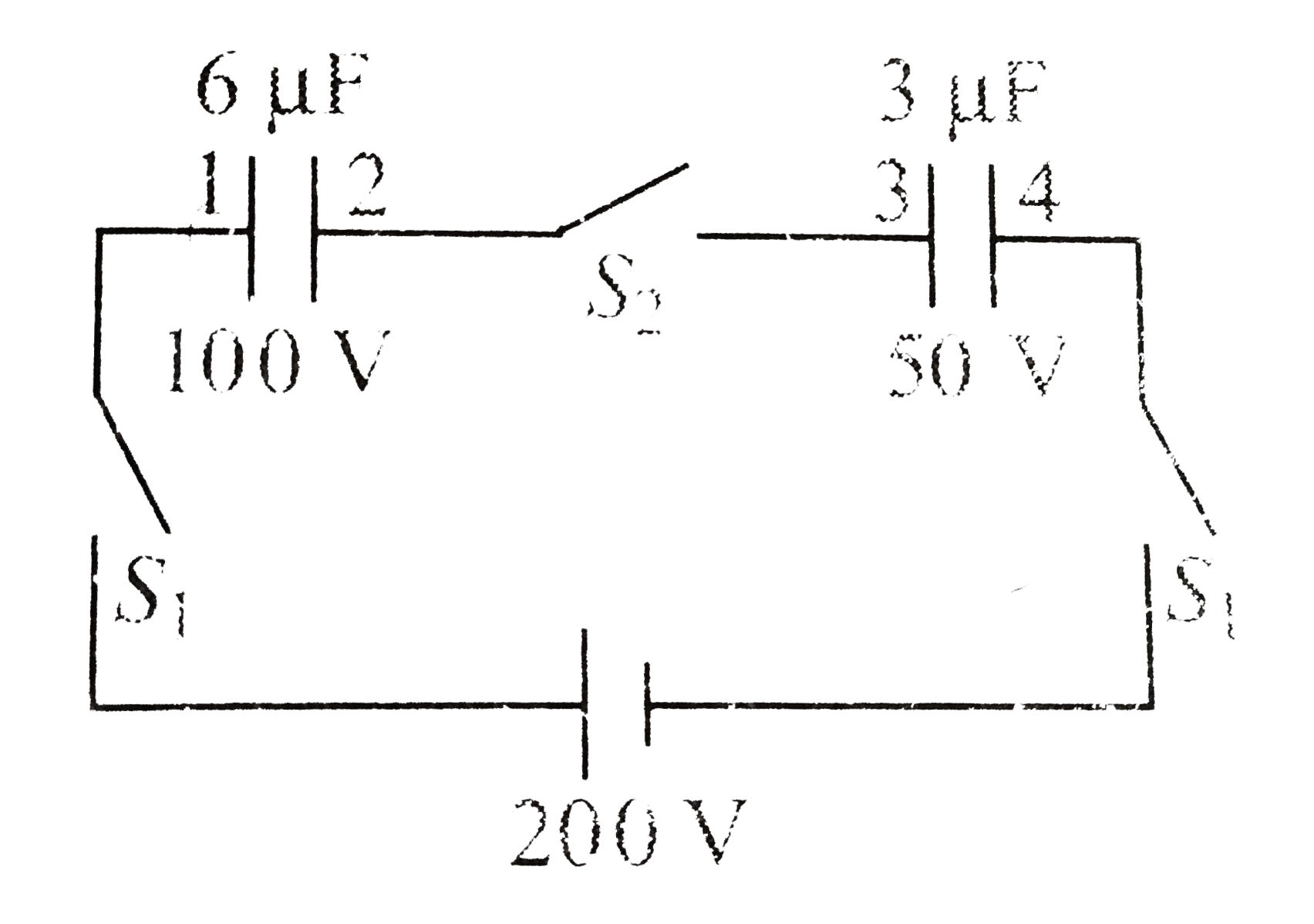
Charges on 6μF And 3μF capacitors in steady state will be
View Solution
