A cyclic quadrilateral KPRQ is inscribed a circle with centre 0. A tangent ST touches the point P. If ∠PRQ=130∘ then ∠QPT=? (Take S and K on the same side of PQ )
Step by step video & image solution for A cyclic quadrilateral KPRQ is inscribed a circle with centre 0. A tangent ST touches the point P. If /_PRQ =130^(@) then /_QPT=? (Take S and K on the same side of PQ ) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
In a circle 0 is the centre.Tangent TPT' touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP)
View SolutionIn a circle 0 is the centre.Tangent TPT touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP )
View Solution
Knowledge Check
- Question 1 - Select One
PQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
A30∘B45∘C60∘D90∘
In a circle 0 is the centre.Tangent TPT' touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP )
View SolutionIn a circle O is the centre.Tangent TPT' touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP )
View SolutionIn a circle, O is the center. Tangent TPT' touches the point P and AP is the chord , if ∠POA =130∘ then the value of ∠APT will be [Take T and A on same side of OP]
View SolutionIn the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
View SolutionIn Figure 4, PQ and PR are tangents drawn to a circle with centre O from an external point P. If ∠PRQ=70∘, then find ∠QPRand∠OQR
View SolutionIn Figure PQ is a chord of a circle with centre O and PT is a tangent. If QPT=60∘ so, find PRQ.
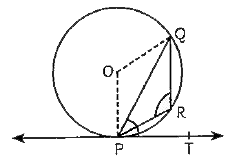 View Solution
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.
 View Solution
View Solution
