In a circle 0 is the centre.Tangent TPT' touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP)
Step by step video & image solution for In a circle 0 is the centre.Tangent TPT' touches the point P and AP is the chord if /_POA=130^(@) then the value of /_APT will be (Take T and A on the same side of OP) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
In a circle O is the centre.Tangent TPT' touches the point P and AP is the chord if ∠POA=130∘ then the value of ∠APT will be (Take T and A on the same side of OP )
View SolutionIn a circle, O is the center. Tangent TPT' touches the point P and AP is the chord , if ∠POA =130∘ then the value of ∠APT will be [Take T and A on same side of OP]
View Solution
Knowledge Check
- Question 1 - Select One
To a circle with centre at 0, two tangents AP and AQ are drawn from an external point A. If the ∠PAQ = 80∘, then the ∠POQ is:
A80∘B70∘C90∘D100∘ - Question 2 - Select One
There are two tangents AT and BT on a circle of radius 30 cm. A line OT(=50 cm) connects the centre O with the external point T. another tangent CD touches the circle at P such that C and D lie on the line segment AT and BT respectively. Points P and T lie on the same side of the circle. find the maximum possible area (in sq. cm) of the circle inscribed in the triangle CDT.
A56.25πB49πC42.25πDnone of these - Question 3 - Select One
AP is tangent to the circle with centre O at point A. OP =10 cm and ∠OPA=30∘. The radiu of the circle is
A10 cmB5√3cmC5 cmD10√3cm
A cyclic quadrilateral KPRQ is inscribed a circle with centre 0. A tangent ST touches the point P. If ∠PRQ=130∘ then ∠QPT=? (Take S and K on the same side of PQ )
View SolutionA cyclic quadrilateral KPRQ is inscribed a circle with centre 0. A tangent ST touches the point P. If ∠PRQ=130∘ then ∠QPT=? (Take S and K on the same side of PQ )
View SolutionAP is tangent to circle O at point P, What is the length of OP?
View SolutionIn the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
 View Solution
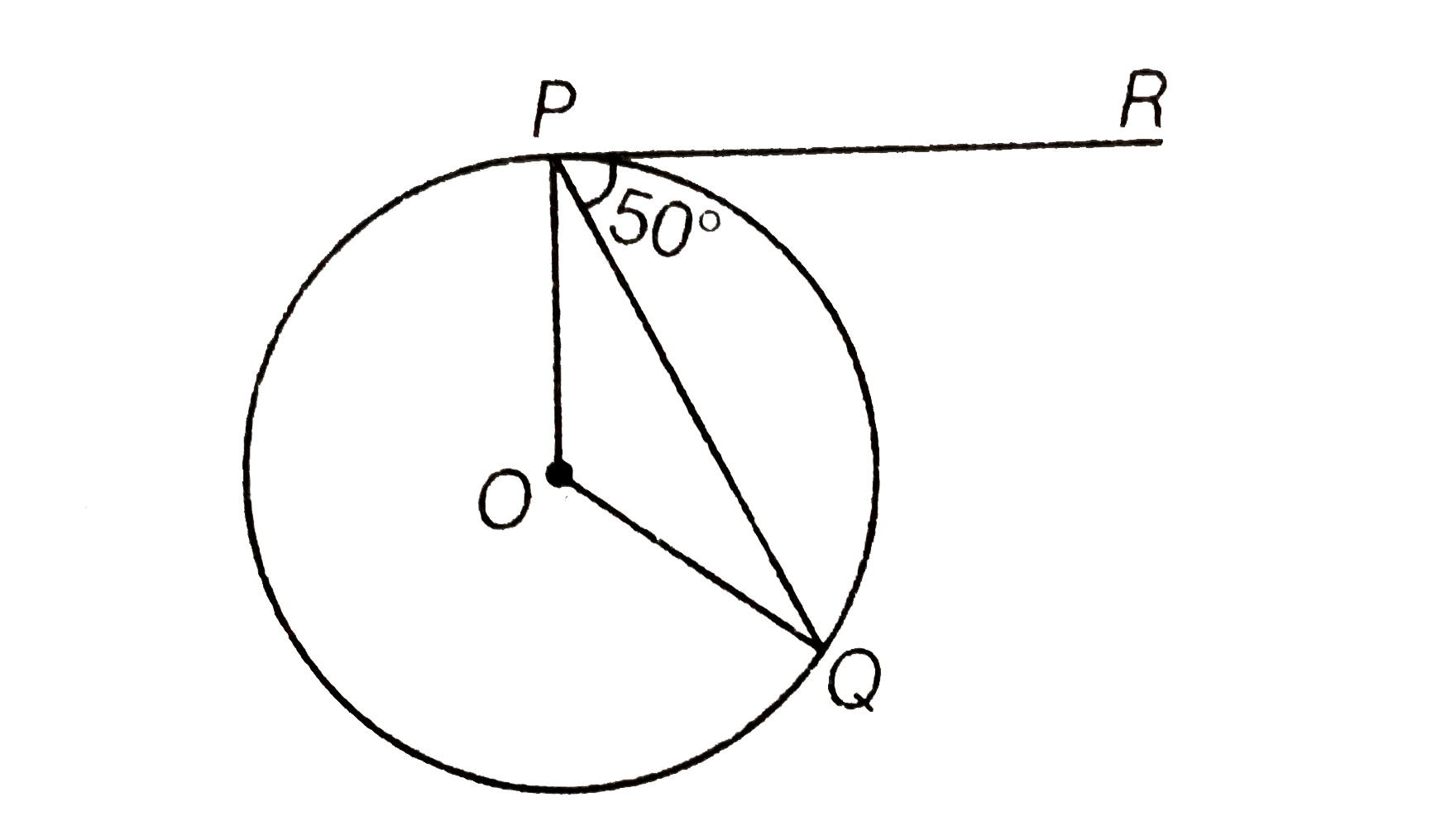
View SolutionIn figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
 View Solution
View Solution
