Once a certain plant begins begins to grow, its height increases at a linear rate. After six weeks, the plant is 54 centimeters tall. Which of the following functions best model the relationship between h(w) the heights in centimeters, of the plant, and w, the number of weeks that the plant has been growing?
h(w)=6w
h(w)=9w
h(w)=54w
h(w)=54+w
The correct Answer is:B
Step by step video, text & image solution for Once a certain plant begins begins to grow, its height increases at a linear rate. After six weeks, the plant is 54 centimeters tall. Which of the following functions best model the relationship between h(w) the heights in centimeters, of the plant, and w, the number of weeks that the plant has been growing? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
This passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
According to the passage, which statement best explains why the Venus flytrap requires a second trigger hair to be touched within a short amount of time in order for its trap to close?View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Based on the passage, a significant advantage of the Venus flytrap’s requirement for multiple triggers is that itView Solution
Knowledge Check
- Question 1 - Select One
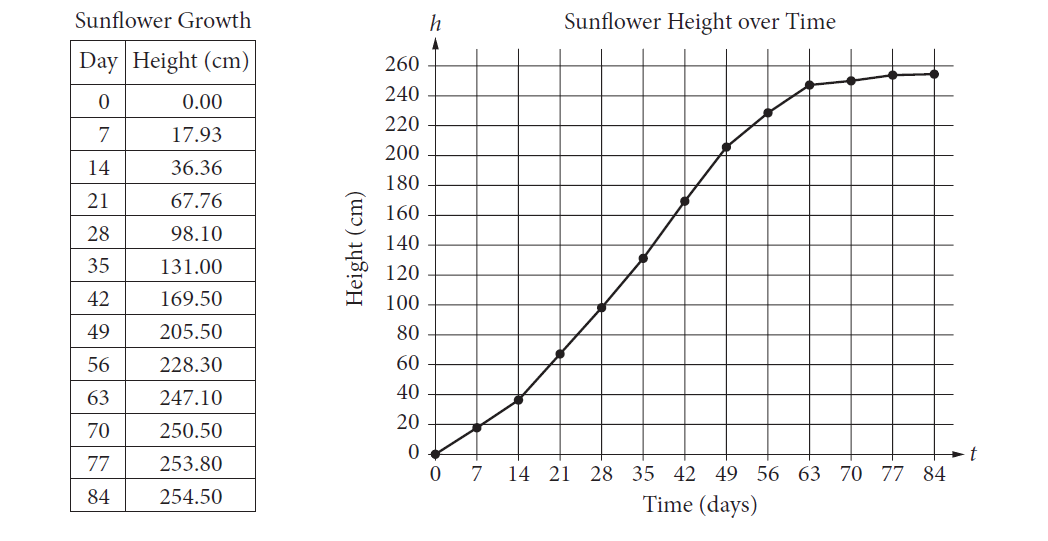
In 1919, H. S. Reed and R. H. Holland published a paper on the growth of sunflowers. Included in the paper were the table and graph above, which show the height h, in centimeters, of a sunflower t days after the sunflower begins to grow.
The growth rate of the sunflower from day 14 to day 35 is nearly constant. On this interval, which of the following equations best models the height h, in centimeters, of the sunflower t days after it begins to grow?Ah = 2.1t − 15Bh = 4.5t − 27Ch = 6.8t − 12Dh = 13.2t − 18 - Question 2 - Select One
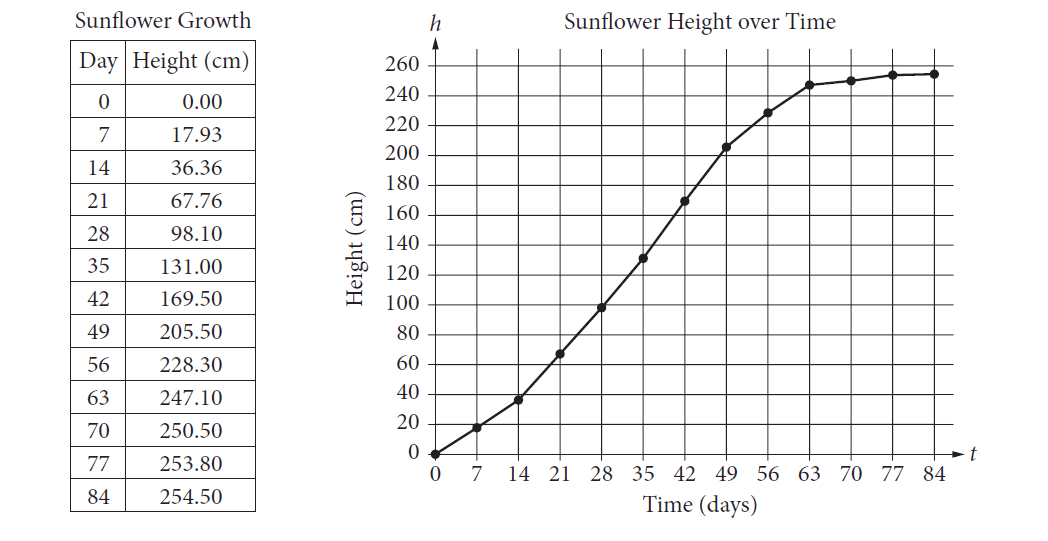
In 1919, H. S. Reed and R. H. Holland published a paper on the growth of sunflowers. Included in the paper were the table and graph above, which show the height h, in centimeters, of a sunflower t days after the sunflower begins to grow.
The function h, defined by h(t) = at + b , where a and b are constants, models the height, in centimeters, of the sunflower after t days of growth during a time period in which the growth is approximately linear. What does a represent?AThe predicted number of centimeters the sunflower grows each day during the periodBThe predicted height, in centimeters, of the sunflower at the beginning of the periodCThe predicted height, in centimeters, of the sunflower at the end of the periodDThe predicted total increase in the height of the sunflower, in centimeters, during the period - Question 3 - Select One
This passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Which choice provides the best evidence for the answer to the previous question?ALines 3-7 (“Closing . . . time”)BLines 7-11 (“The large . . . across the trap”)CLines 11-14 (“If the . . . action”)DLines 16-18 (“First . . . hairs”)
This passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
The use of the phrases “dawdling insect” (line 6), “happily meanders” (line 27), and “unassuming bug’s encounter” (lines 28-29) in the first two paragraphs establishes a tone that isView SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
The primary purpose of the passage is toView SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Based on the passage, in studying the Venus flytrap, Volkov and his colleagues made the most extensive use of which type of evidence?View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
As used in line 67, “demonstrated” most nearly meansView SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Which choice describes a scenario in which Hodick and Sievers’s model predicts that a Venus flytrap will NOT close around an insect?View Solution

