A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :

g2
(√3g)(2)
g√2
g
The correct Answer is:C
x2=4ay,dydx=12ax
at point (2a , 2a) , dydx=1,θ=45∘
Component of weight along tangetial direction is mg sin θ.
Tangential acceleration dvdt=ωdrdt
ω=4π,drdt=0.5 , a = 2π
T−mg=ma,T=mg+ma
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:More than one correct
Explore 18 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Assertion - Reason
Explore 12 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Problem For Practice
Explore 23 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution
Knowledge Check
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
 Ag2B√3g2Cg√2Dg
Ag2B√3g2Cg√2Dg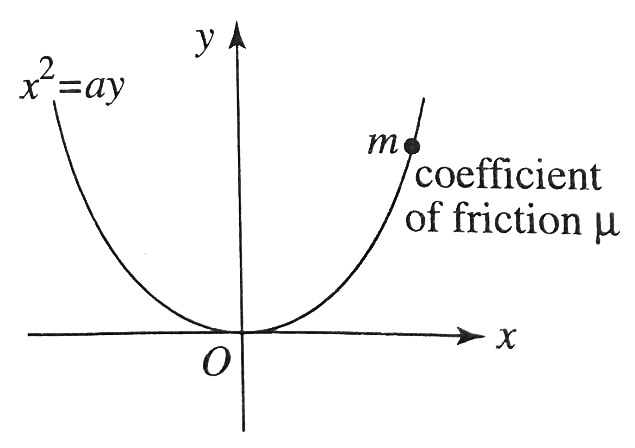
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium isAμaBμ2aC14μ2aD12μa
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium isAμaBμ2aCμ2a4D2μa

A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
View Solution
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
View Solution
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium is
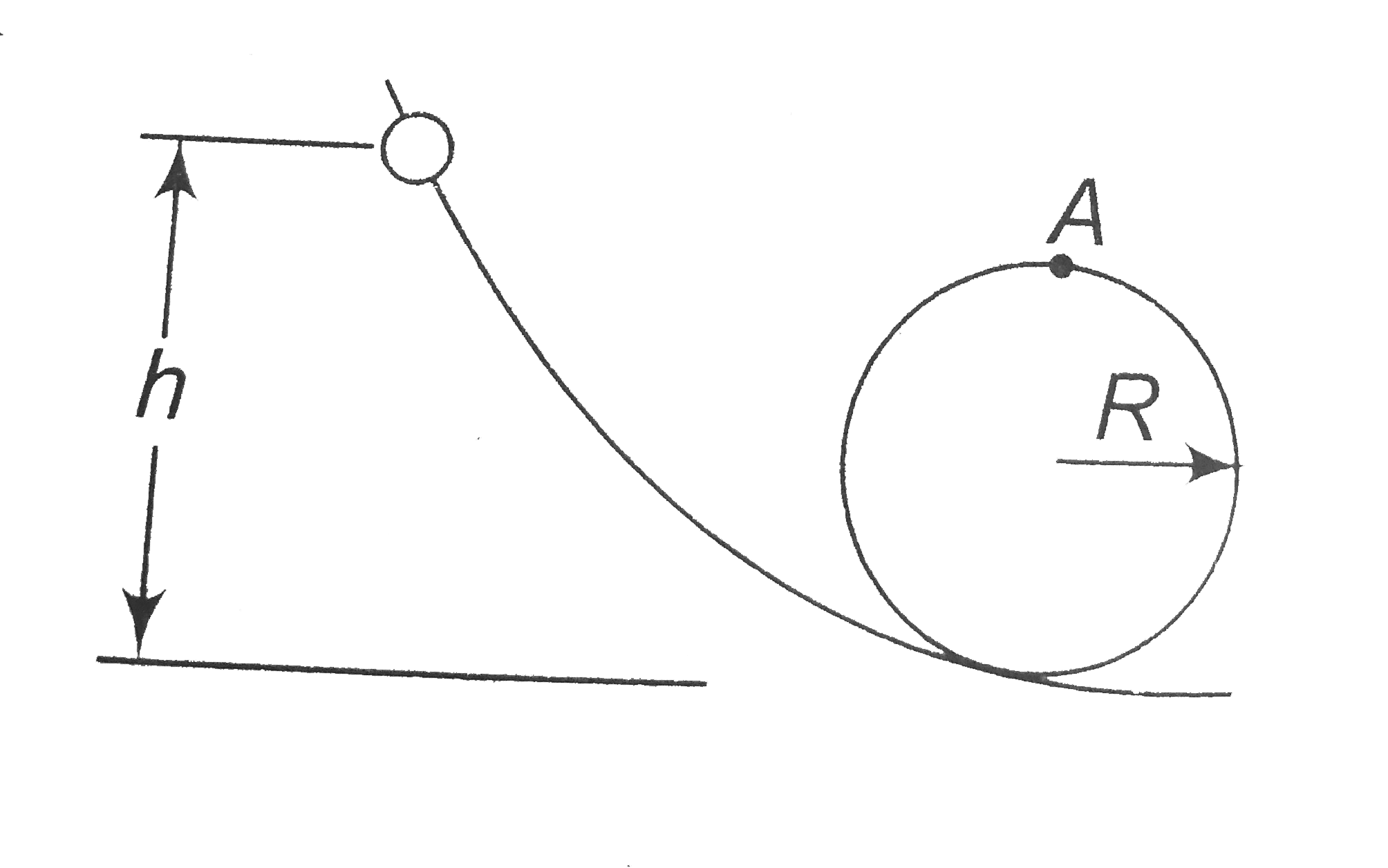
View SolutionA head slide without friction around a loop the (figure). The bead slide is released is from rest at a height h=3.50R. How large is the normal force on the bead at point (A) if its mass is 50g ?
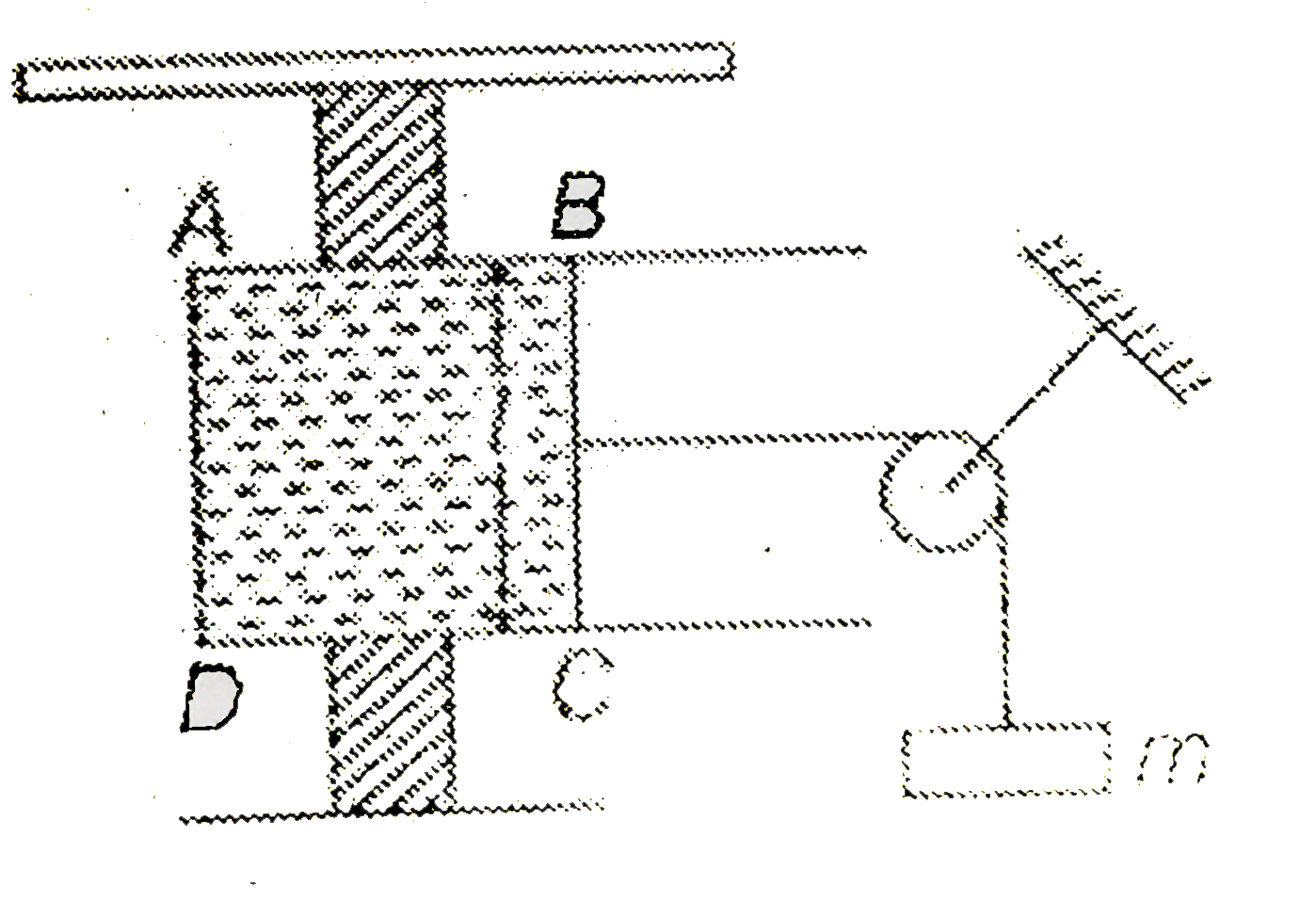
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
View Solution
