[" Two cells of equal e.m.f.and of internal "],[" resistances "r_(1)" and "r_(2)(r_(1)>r_(2))" are "],[" connected in series.On connecting this "],[" combination to an external resistance "R" ,"],[" it is observed that the potential "],[" difference across the first cell becomes "],[" zero.The value of "R" will be "],[[" (A) "r_(2)(r_(1)>r_(2)),(r_(1)+r_(2))/(2)],[" (B) "r_(1)-r_(2),(r_(1)-r_(2))/(2)]]
Step by step video & image solution for [" Two cells of equal e.m.f.and of internal "],[" resistances "r_(1)" and "r_(2)(r_(1)>r_(2))" are "],[" connected in series.On connecting this "],[" combination to an external resistance "R" ,"],[" it is observed that the potential "],[" difference across the first cell becomes "],[" zero.The value of "R" will be "],[[" (A) "r_(2)(r_(1)>r_(2)),(r_(1)+r_(2))/(2)],[" (B) "r_(1)-r_(2),(r_(1)-r_(2))/(2)]] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Two cells of equal e.m.f. E b ut of difference internal resistance r1 and r2 are connected in parallel and the combination is connected with an external resistance R to obtain maximum power in R. find the value of R
 View Solution
View Solution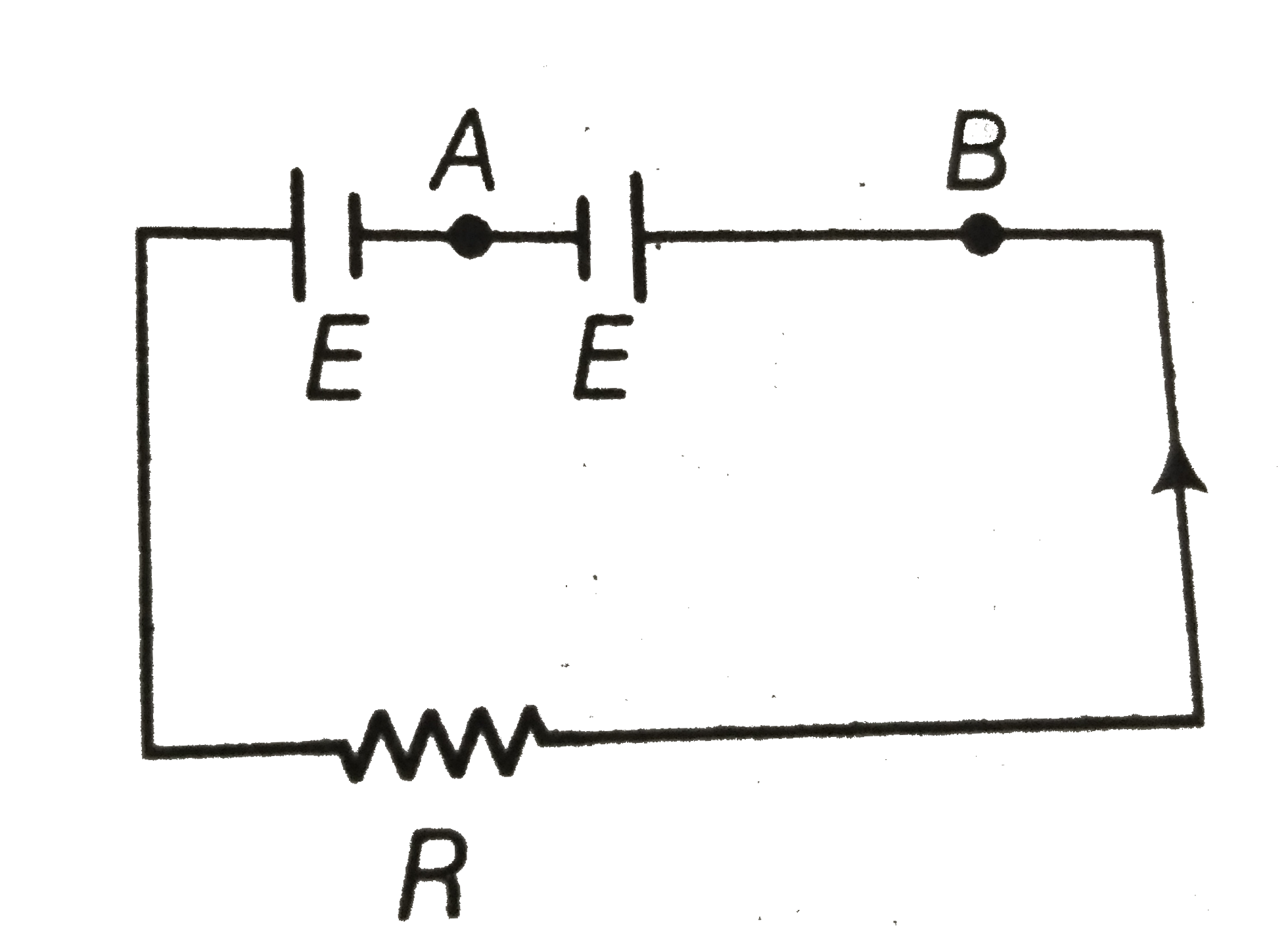
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?View Solution
Knowledge Check
- Question 1 - Select One
Tow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A√r1r2Br1+r2Cr1−r2Dr1+r22 - Question 2 - Select One
Two cell with the same e.m.f. E and difference internal resistance r1andr2 are connected in series to an external resistance R a value of R be selected such that the potential difference as the flow cell E should be zero when
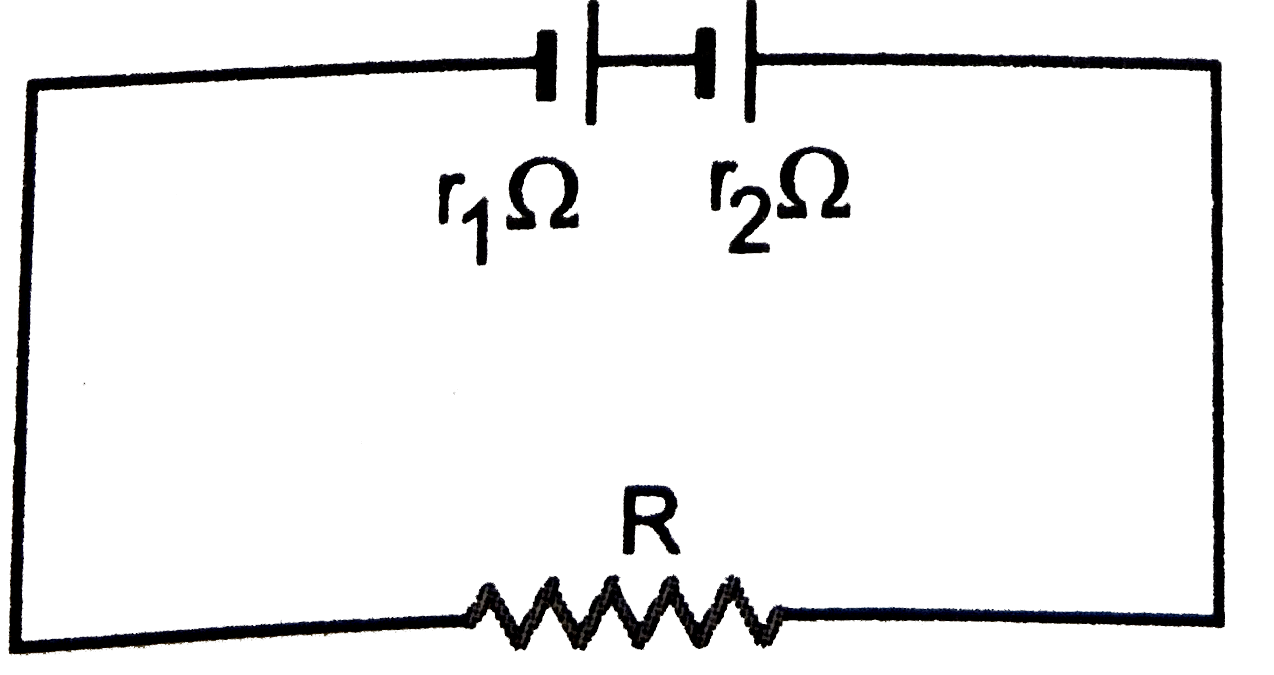 AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2
AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2 - Question 3 - Select One
If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
AV=E/(R+r)BV=ECV=E/(1+r/R)DV=E/(1+R/r)
Two batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
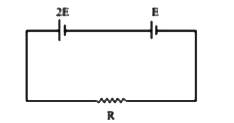
View SolutionTwo cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
 View Solution
View SolutionTwo cells of same emf ε but internal resistances r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
 View Solution
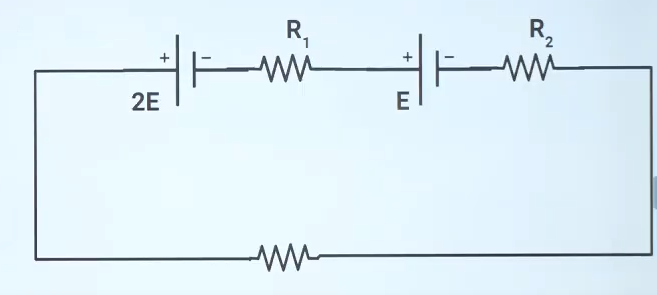
View SolutionInternal resistance of battery of emf 2E is R1 and battery of emf E is R2. If the potential difference across the cell of emf 2E is zero, then value of R is
 View Solution
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
 View Solution
View Solution
