Twenty-one people were playing a game. 1 person scored 50 points, 2 people scored 60 points, 3 people scored 70 points, 4 people scored 80 points, 5 people scored 90 points, and 6 people scored 100 points. Which of the following correctly shows the order of the median, mode and average (arithmetic mean) of the 21 scores?
The correct Answer is:A
To solve the problem, we need to find the median, mode, and average (arithmetic mean) of the scores of 21 people who played a game. Let's go through the steps one by one.
Step 1: List the Scores
We have the following scores based on the number of people who scored them:
- 1 person scored 50 points
- 2 people scored 60 points
- 3 people scored 70 points
- 4 people scored 80 points
- 5 people scored 90 points
- 6 people scored 100 points
We can list all the scores in ascending order:
- 50 (1 time)
- 60 (2 times)
- 70 (3 times)
- 80 (4 times)
- 90 (5 times)
- 100 (6 times)
Thus, the complete list of scores is:
50, 60, 60, 70, 70, 70, 80, 80, 80, 80, 90, 90, 90, 90, 90, 100, 100, 100, 100, 100, 100
Step 2: Calculate the Average (Arithmetic Mean)
To find the average, we need to sum all the scores and divide by the total number of scores.
Sum of Scores Calculation:
- 1×50=50
- 2×60=120
- 3×70=210
- 4×80=320
- 5×90=450
- 6×100=600
Now, add these values together:
50+120+210+320+450+600=1750
Average Calculation:
Average=Total Sum of ScoresTotal Number of Scores=175021≈83.33
Step 3: Calculate the Mode
The mode is the score that occurs most frequently. From our list of scores:
- 100 occurs 6 times (the highest frequency).
Thus, the mode is:
Mode=100
Step 4: Calculate the Median
To find the median, we need to determine the middle score in our ordered list. Since there are 21 scores (an odd number), the median is the score at the position:
Median Position=n+12=21+12=11
Now, we count to the 11th score in our ordered list:
1. 50
2. 60
3. 60
4. 70
5. 70
6. 70
7. 80
8. 80
9. 80
10. 80
11. 90
Thus, the median is:
Median=90
Step 5: Order the Values
Now we have:
- Average = 83.33
- Median = 90
- Mode = 100
Ordering these values from smallest to largest:
1. Average: 83.33
2. Median: 90
3. Mode: 100
Final Answer
The correct order of the median, mode, and average is:
Average<Median<Mode
We have the following scores based on the number of people who scored them:
- 1 person scored 50 points
- 2 people scored 60 points
- 3 people scored 70 points
- 4 people scored 80 points
- 5 people scored 90 points
- 6 people scored 100 points
- 50 (1 time)
- 60 (2 times)
- 70 (3 times)
- 80 (4 times)
- 90 (5 times)
- 100 (6 times)
50, 60, 60, 70, 70, 70, 80, 80, 80, 80, 90, 90, 90, 90, 90, 100, 100, 100, 100, 100, 100
To find the average, we need to sum all the scores and divide by the total number of scores.
- 1×50=50
- 2×60=120
- 3×70=210
- 4×80=320
- 5×90=450
- 6×100=600
50+120+210+320+450+600=1750
Average=Total Sum of ScoresTotal Number of Scores=175021≈83.33
The mode is the score that occurs most frequently. From our list of scores:
- 100 occurs 6 times (the highest frequency).
Mode=100
To find the median, we need to determine the middle score in our ordered list. Since there are 21 scores (an odd number), the median is the score at the position:
Median Position=n+12=21+12=11
Now, we count to the 11th score in our ordered list:
1. 50
2. 60
3. 60
4. 70
5. 70
6. 70
7. 80
8. 80
9. 80
10. 80
11. 90
Median=90
Now we have:
- Average = 83.33
- Median = 90
- Mode = 100
1. Average: 83.33
2. Median: 90
3. Mode: 100
The correct order of the median, mode, and average is:
Average<Median<Mode
Similar Questions
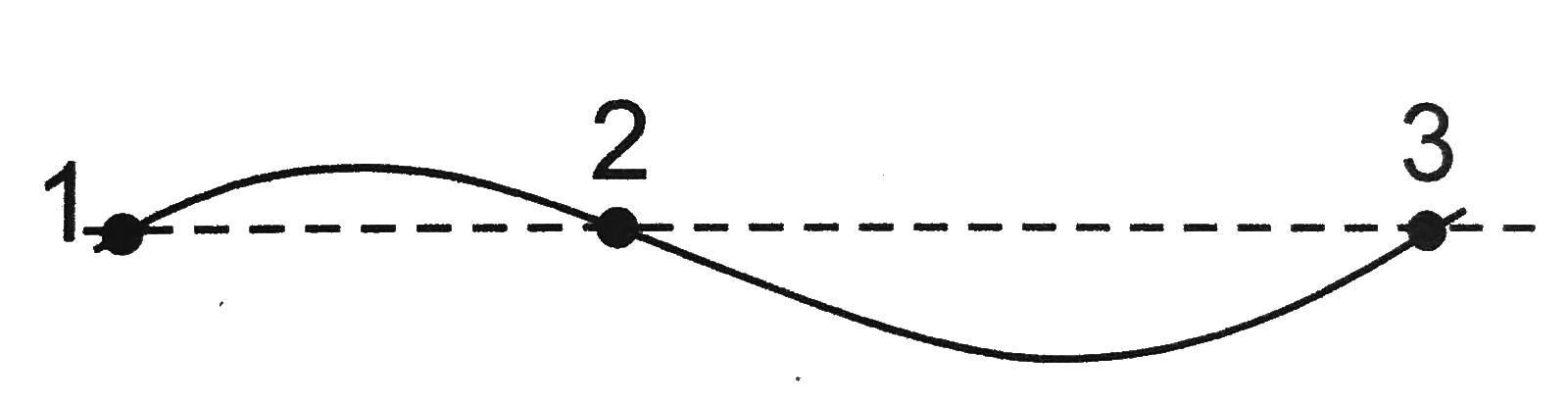
The diagram below shows an instantaneous position of a string as a transverse progressive wave travels along it from left to right Which one of the following correctly shows the direction of the velocity of the points 1,2 and 3 on the string?
View SolutionThe mean score of 8 players in a basketball game was 14.5 points. IF the highest individual score is removed, the mean score of the remaining 7 players becomes 12 points. What was the highest score?
View Solution
Knowledge Check
Jackson High School's basketball team scored an average of 90 points in each of the first 10 games of the season. If it scored 102 points in each of the next 2 games , which of the following is closest to its average for all 12 games ?
A102B98C96D92Mela earned scores of 75, 70, 92, 95 and 97 points (a total of 429 points) on the first 5 tests in Economics II. Solving which of the following equations for s gives the score he needs to earn on the 6th test to average exactly 85 points for all 6 tests?
A4295+s=85B4296+s=85Cs+4295=85D(s + 429)/6 = 85the arithmetic mean of a set of 20 test scores is represented by x. If each scores is increased by y points, which expression represents the arithmetic mean of the revised set of test scores?
Ax+yBx+20yCx+y20Dx+y20
The total score in a football game was 72 points. The winning team scored 12 points more than the closing team. How many points did the winning team score?
View SolutionIn an exam , 3.5 points are awarded for evey correct answer and 0.45 points are deducted for every wrong answer. If out of N question , a boy answers at least 4 questions wrong and at most 8 questions wrong ,which of the following correctly gives the correct range of score ,S, he can get in the exam ?
View SolutionDuring the NBA playoffs, Chicago Bulls , last year's basketball champion, scored 88 points in their fifth game of the season. As a result their average points increased by an integer value from what is initially was in that season. Which of the following could have been their initial average points scored in the initial four game in the season ?
View Solution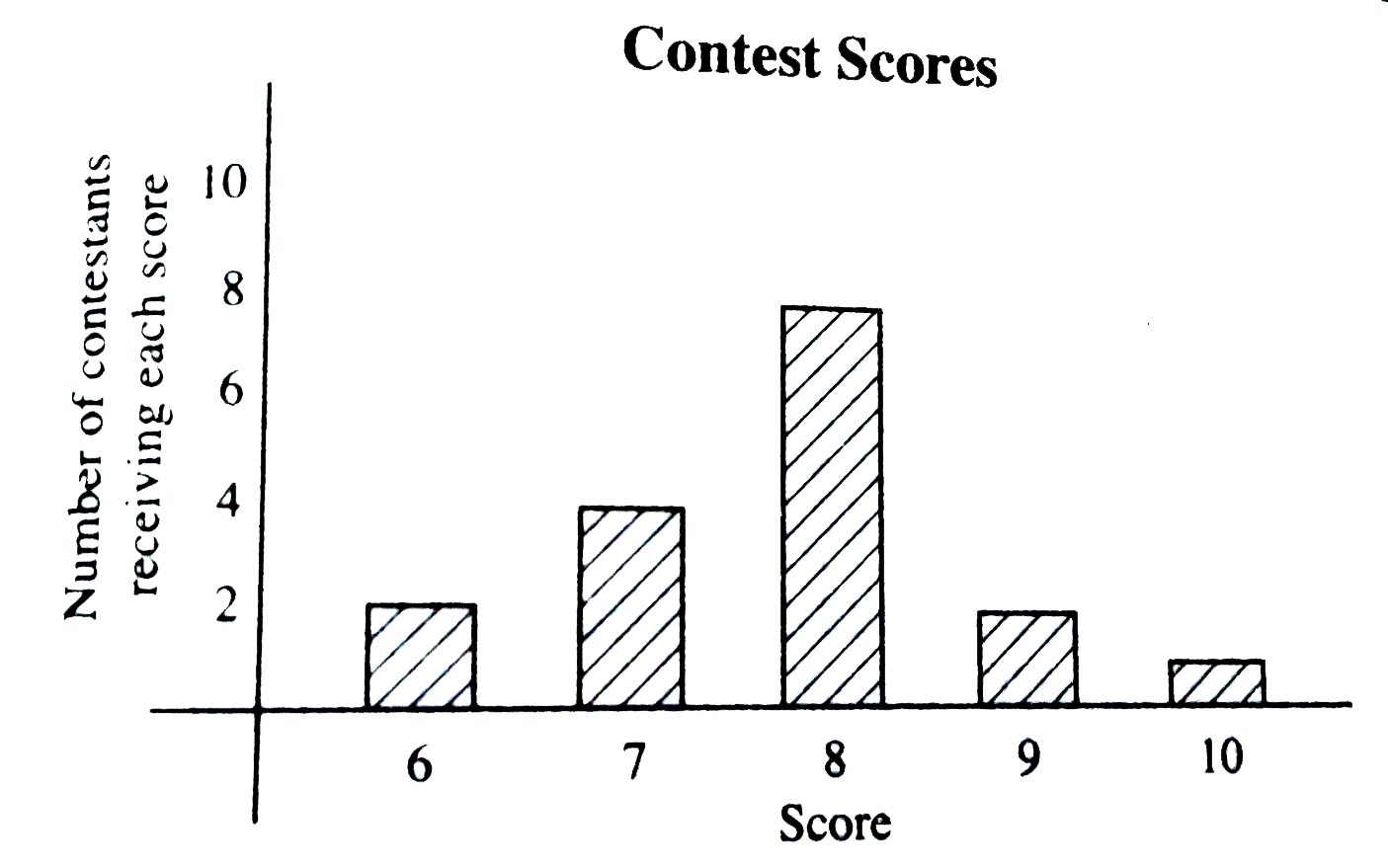
In a contest , each contestant could receive a score of 6,7,8,9, or 10. The bar graph above shows how many contestants received each score .
The score of 8 is described by which of the following measures ?
I.The average (arithmetic mean )
II.The median
III.The mode
View SolutionIn a video game, each player starts the game with k points and loses 2 points each time a task is not completed. If a player who gains no additional points and fails to complete 100 tasks has a score of 200 points, what is the value of k ?
View Solution
