In the figure, ABCD is a square and EF is parallel to BD. R is the mid-point of EF. Prove that (i) BE= DF (ii) AR bisects ∠BAD and (iii) If AR is produced it will pass through C.
Step by step video & image solution for In the figure, ABCD is a square and EF is parallel to BD. R is the mid-point of EF. Prove that (i) BE= DF (ii) AR bisects /_BAD and (iii) If AR is produced it will pass through C. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
ABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that :
(i) BE=DF
(ii) AR bisects angle BAD
(iii) If AR produced it will pass through C.
View SolutionABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that :
(i) BE=DF
(ii) AR bisects angle BAD
(iii) If AR produced it will pass through C.
View Solution
Knowledge Check
In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
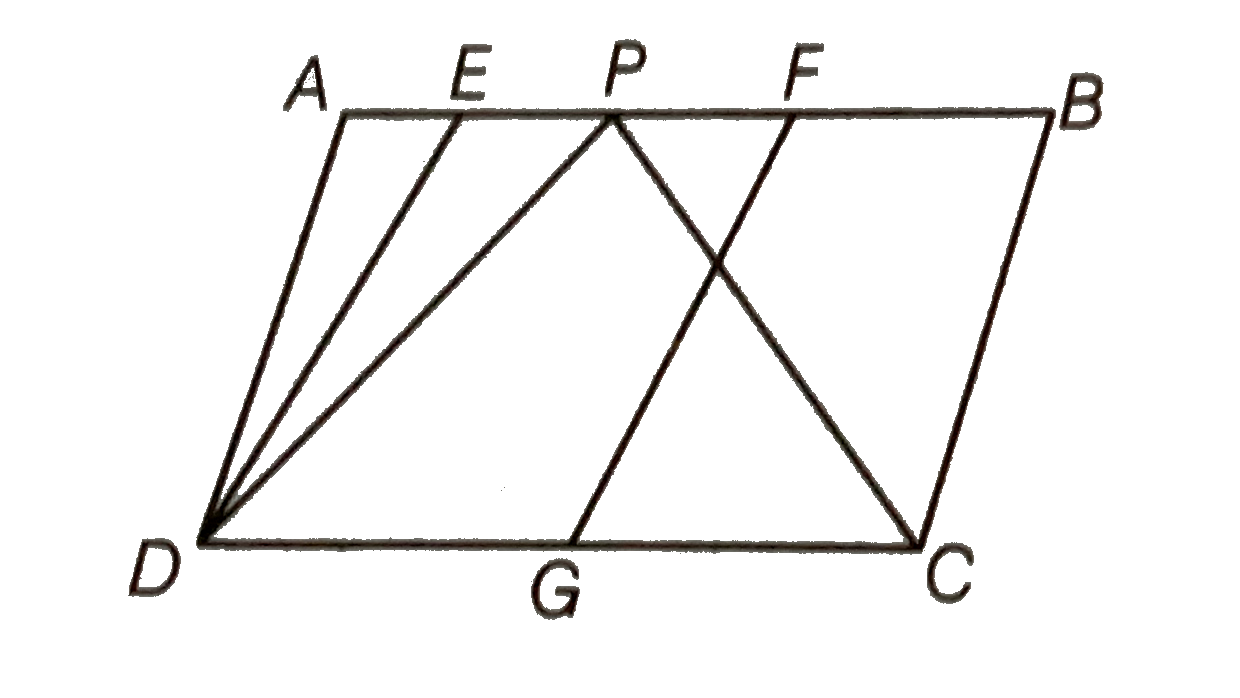ATrueBFalseCPartially trueDNone of these
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
View SolutionIn the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
EF=FB
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
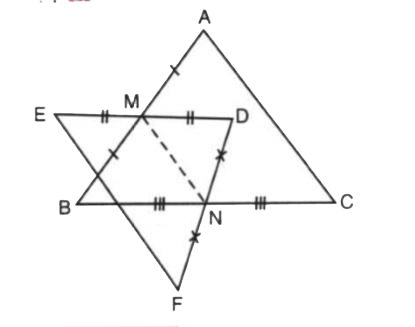
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
ar(ΔAEDF) = ar(ΔABCDE)
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
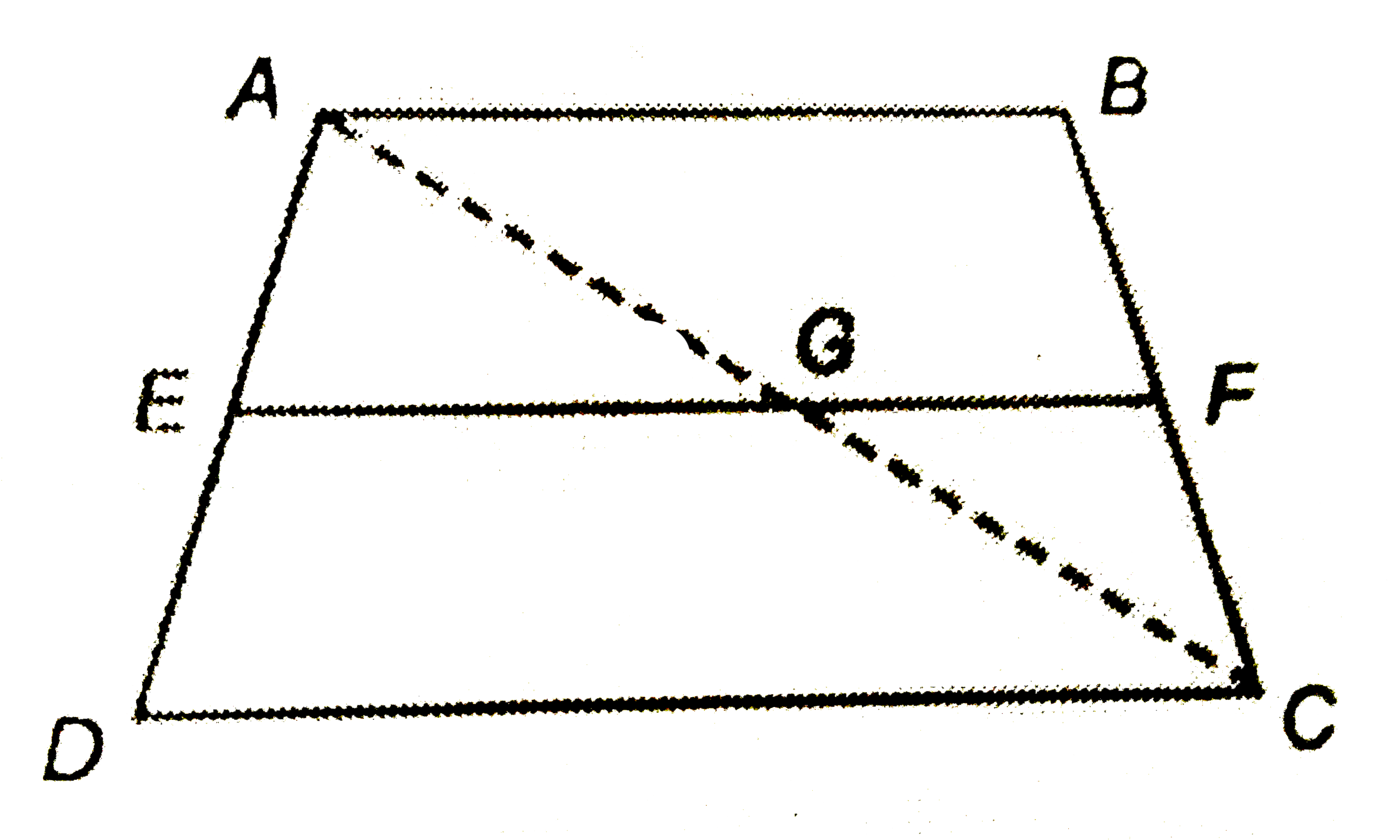
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
View Solution