चित्र में, ABCD तथा AEFD दो समांतर चतुर्भुज है। सिद्ध कीजिए कि :
(i) PE=FQ
( ii) ar(ΔAPE):ar(ΔPEA)=ar(ΔQFD):ar(ΔPFD)
(iii) ar(ΔPEA)=ar(ΔQFD)
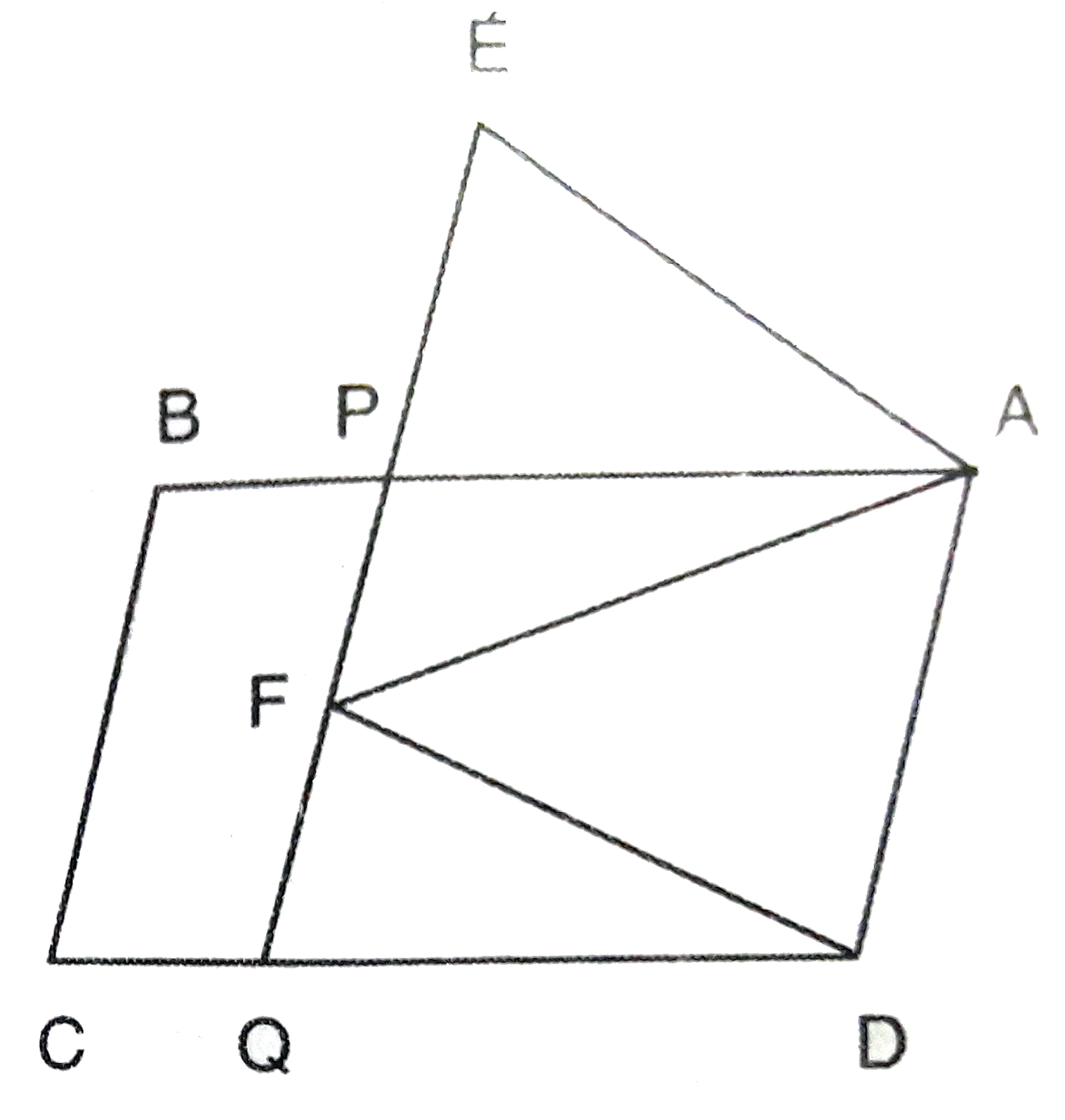
(i) त्रिभुज APE तथा त्रिभुज DQF पर विचार करते है। इन दोनों त्रिभुजों में
∠APE=∠DQF
AE=DF
∠AEP=∠DFQ
अतः कोण-कोण-भुजा सर्वांगसम अभिगृहित से,
ΔAPE≅ΔDQF
⇒PE=QF तथा ar(ΔAPE)=ar(ΔDQF) ...(i)
इस प्रकार (i ) और (iii ) सत्यापित हो जाते है।
(ii ) स्पष्ट है कि त्रिभुज PFA तथा त्रिभुज PFD एक ही आधार PF पर और एक ही समांतर रेखाओं PQ और AD के बीच स्थित है।
∴ar(ΔPFA)=ar(ΔPFD) ...(ii)
(i ) तथा (ii ) से ,
ar(ΔAPE)ar(ΔPFA)=ar(ΔDQF)ar(ΔPFD)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघुत्तरात्मक प्रश्न
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.2
4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
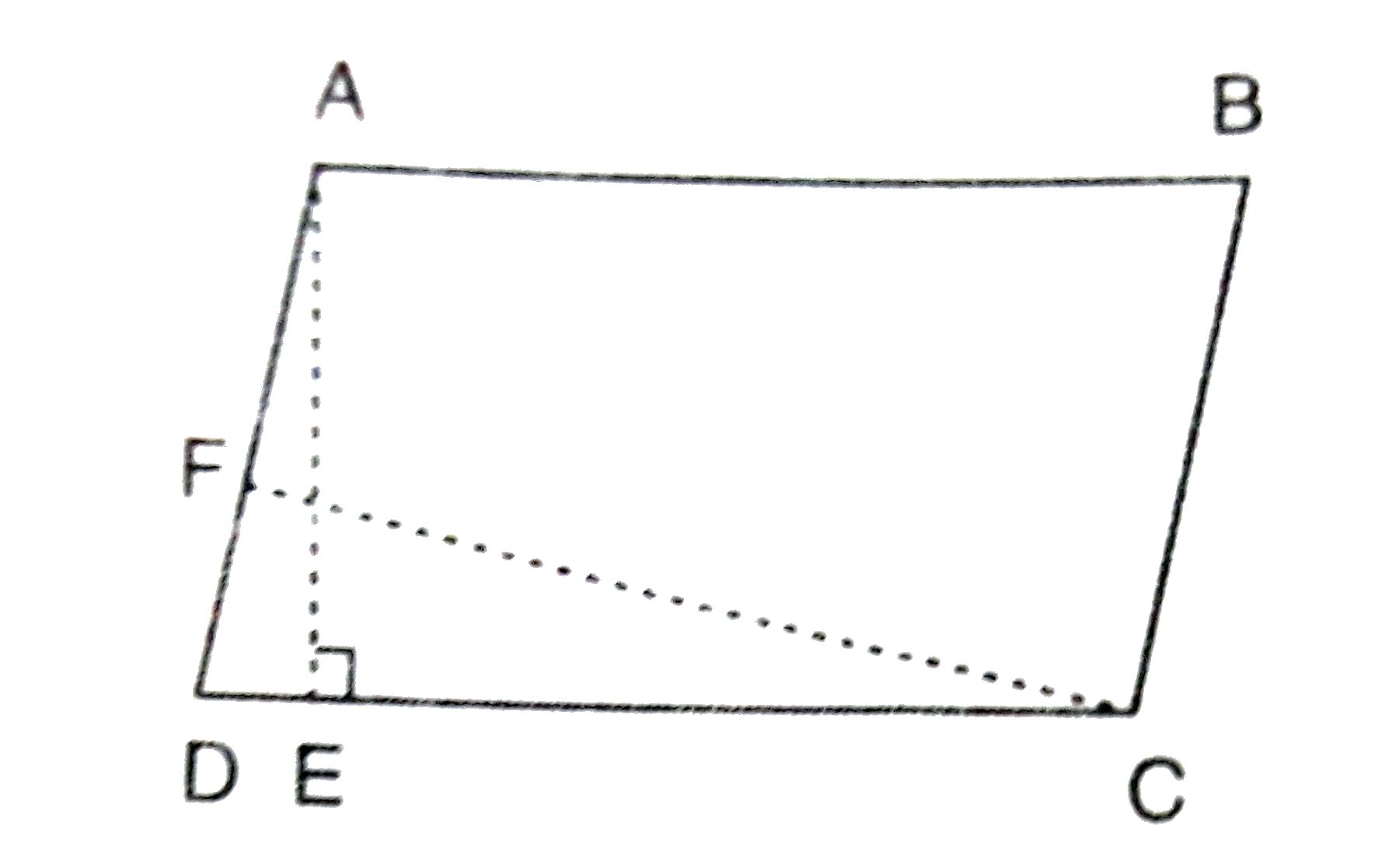
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
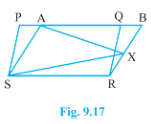
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)
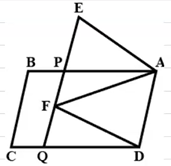
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View Solutionआकृति में, PQRS और ABRS समांतर चतुर्भुज है तथा X भुजा BR स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(PQRS)=ar(ABRS)
(ii) ar(AXS)=12ar(PQRS)
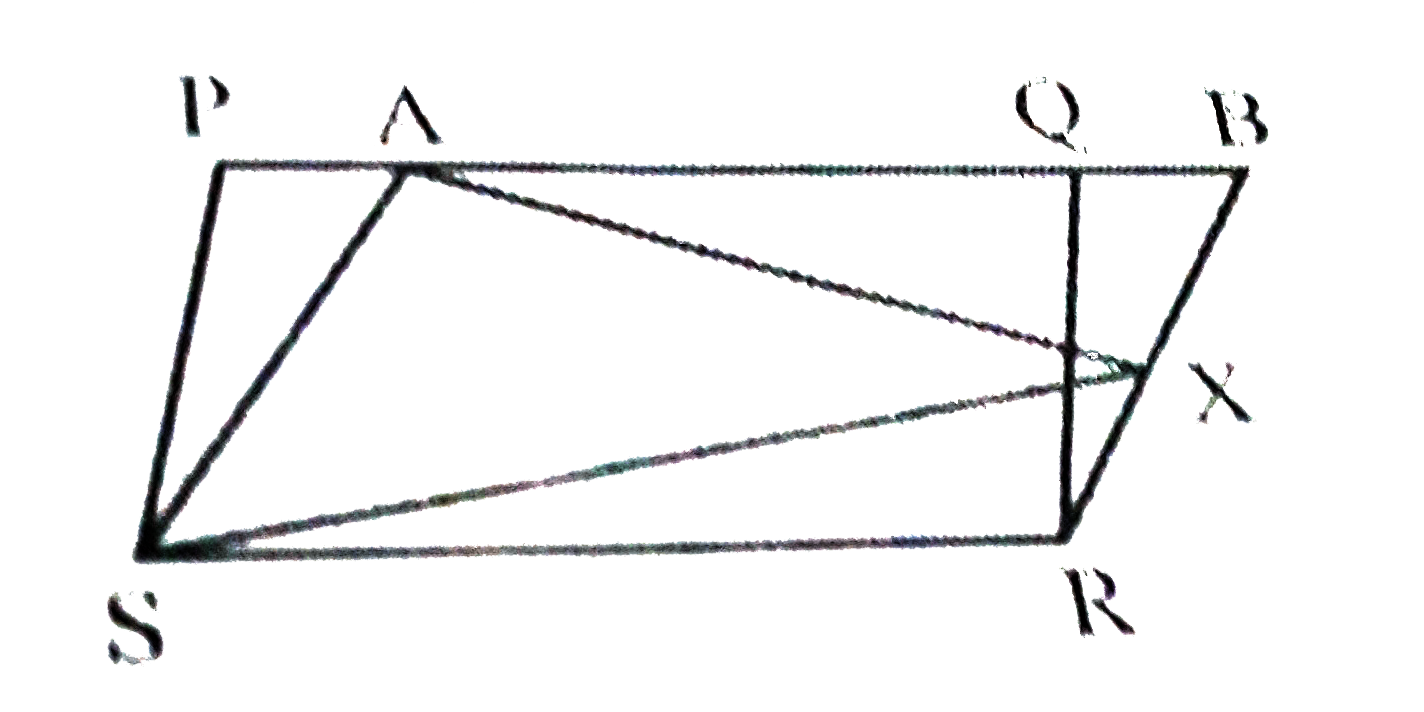
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
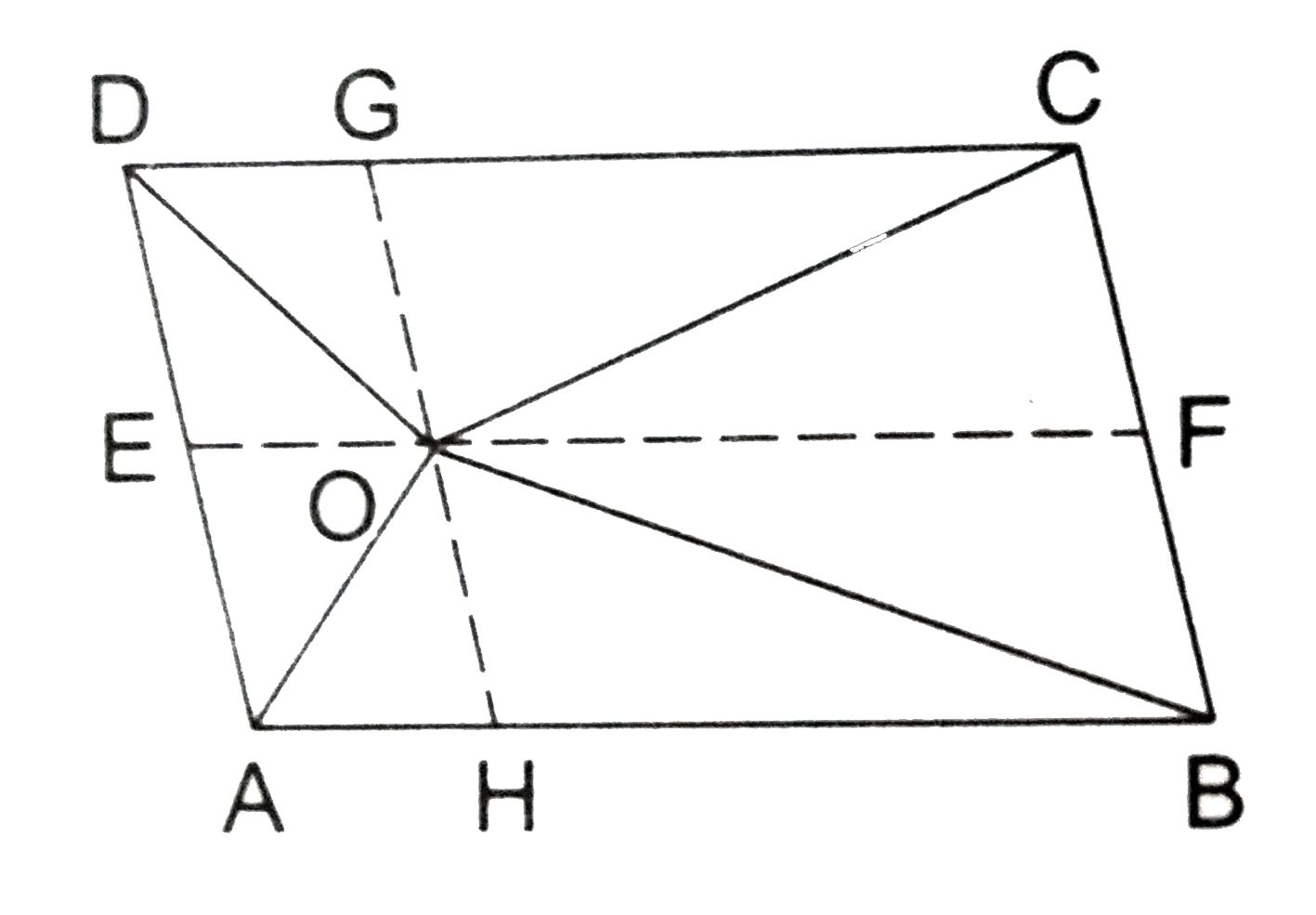
View Solutionचित्र में PQRS तथा ABRS समान्तर चतुर्भुज है तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाए कि
(i)ar(||gmPQRS)=ar(||gmABRS) (ii)ar(ΔAXS)=12ar(||gmPQRS)
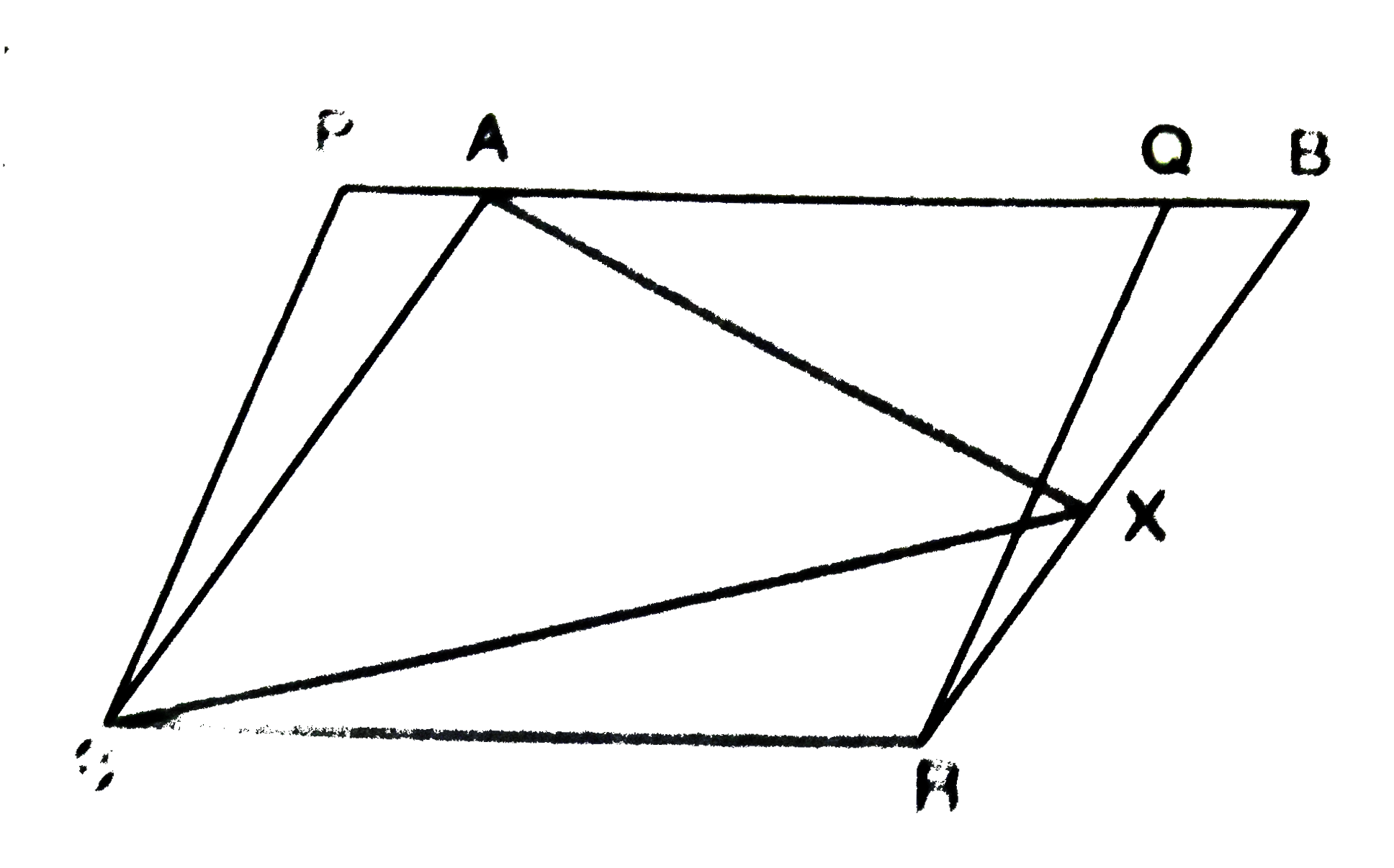
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
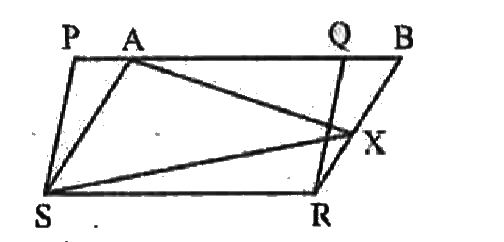
View SolutionFactorise:
ar+br+at+bt
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View Solution
