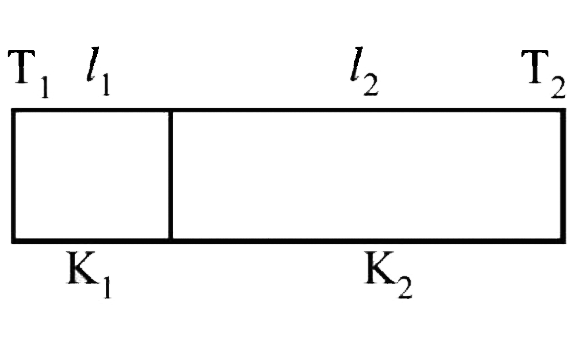
One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

$(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2}) / (k_{1} l_{1} + k_{2} l_{2})$

$(k_{2} l_{1} T_{1} + k_{1} l_{2} T_{2}) / (k_{2} l_{1} + k_{1} l_{2})$

$(k_{1} l_{2} T_{1} + k_{1} l_{2} T_{2}) / (k_{1} l_{2} + k_{2} l_{1})$

$(k_{1} l_{1} T_{1} + k_{2} l_{2} T_{2}) / (k_{1} l_{1} + k_{2} l_{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video & image solution for One end of a thermally insulated rod is kept at a temperature T_1 and the other at T_2. The rod is composed of two sections of length l_1 and l_2 and thermal conductivities K_1 and K_2 respectively. The temperature at the interface of the two section is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS HEAT TRANSFER & THERMAL EXPANSION

Topper's Solved these Questions

Knowledge Check

One end of thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two section of length $l_{1}$ and $l_{2}$ thermal conductivities $k_{1}$ and $k_{2}$ respectively. The temerature at the interface of two section is
A $\frac{(k_{1} l_{1} T_{1} + k_{2} l_{2} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
B $\frac{(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
C $\frac{(k_{2} l_{1} T_{1} + k_{1} l_{2} T_{2})}{(k_{2} l_{1} + k_{1} l_{2})}$
D $\frac{(k_{1} l_{2} T_{1} + k_{2} l_{1} T_{2})}{(k_{1} l_{2} + k_{2} l_{1})}$
Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is
A $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
B $(K_{1} + K_{2})$
C $\frac{K_{1} + K_{2}}{2}$
D $\sqrt{K_{1} K_{2}}$
Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is
A $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
B $(K_{1} + K_{2})$
C $\frac{K_{1} + K_{2}}{2}$
D $\sqrt{K_{1} K_{2}}$

MOTION-HEAT TRANSFER & THERMAL EXPANSION -Exercise - 3 Section-B

Home
Ask Doubt
Profile

One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

One end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is

Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is

Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is

MOTION-HEAT TRANSFER & THERMAL EXPANSION -Exercise - 3 Section-B

One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

One end of thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two section of length $l_{1}$ and $l_{2}$ thermal conductivities $k_{1}$ and $k_{2}$ respectively. The temerature at the interface of two section is

Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is

Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is