Comparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table
The correct Answer is:(A) Q, (B) T, (C) R, (D) T
To solve the problem of matching LC oscillations with spring-block oscillations, we will analyze the equations governing both systems and identify their corresponding parameters.
Step 1: Understand the equations of motion
For the spring-block system, the equation of motion is given by:
md2xdt2+kx=0
where:
- m is the mass of the block,
- k is the spring constant,
- x is the displacement.
For LC oscillations, the equation of motion is:
Ld2Idt2+1CQ=0
where:
- L is the inductance,
- C is the capacitance,
- I is the current,
- Q is the charge.
Step 2: Identify corresponding parameters
1. Mass (m) and Inductance (L):
- In the spring-block system, m is the mass.
- In LC oscillations, L plays a similar role to mass in terms of inertia in the oscillation.
- Therefore, m corresponds to L.
2. Spring constant (k) and Capacitance (C):
- The spring constant k in the spring-block system is analogous to the capacitance C in LC oscillations.
- The relationship can be noted as k∼1C.
- Thus, k corresponds to 1C.
3. Displacement (x) and Charge (Q):
- Displacement x in the spring-block system corresponds to the charge Q in LC oscillations.
- Therefore, x corresponds to Q.
4. Velocity (v) and Current (i):
- The velocity v in the spring-block system is the rate of change of displacement, v=dxdt.
- The current i in LC oscillations is the rate of change of charge, i=dQdt.
- Hence, v corresponds to i.
5. Acceleration and Rate of Change of Current:
- The acceleration in the spring-block system is given by d2xdt2.
- In LC oscillations, the rate of change of current can be represented as didt.
- Therefore, acceleration corresponds to didt.
Step 3: Match the parameters
Now we can summarize the matches:
- A (L) matches with P (k)
- B (C) matches with Q (m)
- C (i) matches with R (v)
- D (di/dt) matches with S (x)
Final Matching Table
| Table-1 (LC oscillations) | Table-2 (Spring-block oscillations) |
|---------------------------|-------------------------------------|
| A (L) | P (k) |
| B (C) | Q (m) |
| C (i) | R (v) |
| D (di/dt) | S (x) |
md2xdt2+kx=0
where:
- m is the mass of the block,
- k is the spring constant,
- x is the displacement.
Ld2Idt2+1CQ=0
where:
- L is the inductance,
- C is the capacitance,
- I is the current,
- Q is the charge.
- In the spring-block system, m is the mass.
- In LC oscillations, L plays a similar role to mass in terms of inertia in the oscillation.
- Therefore, m corresponds to L.
- The spring constant k in the spring-block system is analogous to the capacitance C in LC oscillations.
- The relationship can be noted as k∼1C.
- Thus, k corresponds to 1C.
- Displacement x in the spring-block system corresponds to the charge Q in LC oscillations.
- Therefore, x corresponds to Q.
- The velocity v in the spring-block system is the rate of change of displacement, v=dxdt.
- The current i in LC oscillations is the rate of change of charge, i=dQdt.
- Hence, v corresponds to i.
- The acceleration in the spring-block system is given by d2xdt2.
- In LC oscillations, the rate of change of current can be represented as didt.
- Therefore, acceleration corresponds to didt.
- A (L) matches with P (k)
- B (C) matches with Q (m)
- C (i) matches with R (v)
- D (di/dt) matches with S (x)
|---------------------------|-------------------------------------|
| A (L) | P (k) |
| B (C) | Q (m) |
| C (i) | R (v) |
| D (di/dt) | S (x) |
Similar Questions
Comparing the L-C oscillations with the oscillations of a spring-block system
View SolutionWhile comparing the L−C oscillations with the oscillations of spring-block system, with whom the magnetic energy can be compared and why?
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View SolutionName the block speses A,B,C and D given in the following table

View SolutionMatch the following
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)Stress×Strain(P)J(B)YAl(Q)N/m(C)Yl3(R)J/m3(D)FlAY(S)m∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionMatch the following
Table-1Table-2(A)L(P)[M0L0T−2](B)Magnetic Flux(Q)[ML2T−2A−1](C)LC(R)[ML2T−2A−2](D)CR2(S)None
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
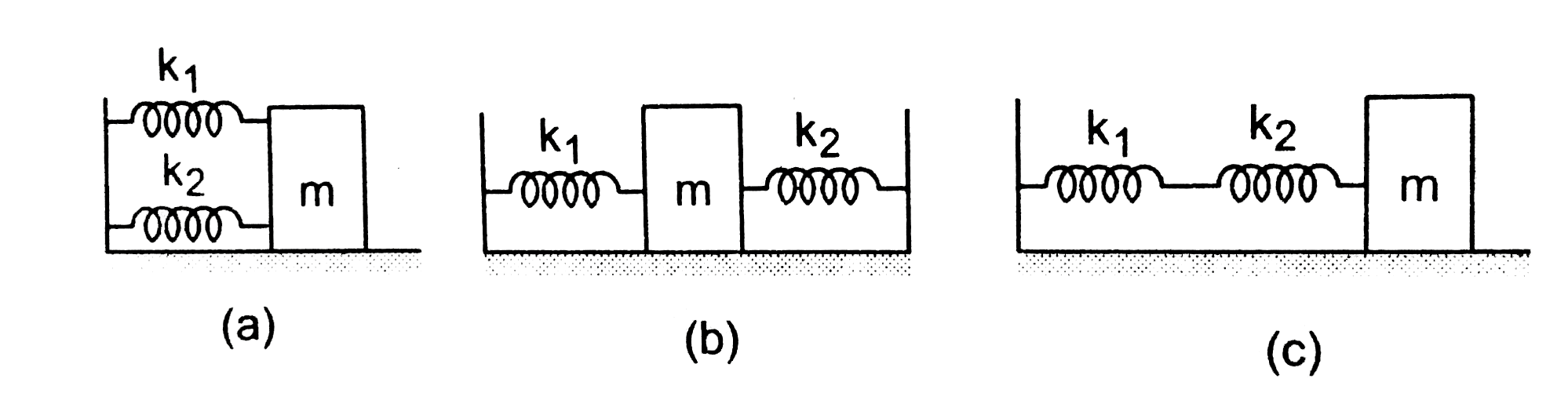
View SolutionMatch the following
Table - 1Table - 2(A)σ2/ε0(P)C2/J−m(B)ε0(Q)Farad(C)ampere - secondVolt(R)J/m3(D)VE(S)metre
View SolutionA spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View Solution